
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Методичні поради
Методичні поради
Якість роботи цифрових систем автоматичного управління визначається такими ж показниками, як і якість неперервних систем. Основними з них є: усталена (статична) похибка, величина максимального перерегулювання та час перехідного процесу.
Статичну похибку можна обчислити, використавши теорему про кінцеве значення оригіналу дискретного перетворення Лапласа:
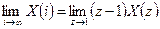
де
Х(і) - дискретні значення функції X;
X(z) - z-зображення цієї функції.
Таблиця 3.1
Параметри досліджуваних систем до лабораторної роботи № 3
| № з/п | Схема на рис. 3.1 | К1 | К2 | К3 | Т1, с | Т2, с | Т3, с | Т, с |
| А | 0,5 | 2,5 | 2,5 | - | 0,025 | |||
| Б | 0,4 | 0,5 | 0,05 | |||||
| В | 0,1 | 0,4 | - | 0,05 | ||||
| а | 0,75 | 0,6 | 1,8 | 0,5 | 0,54 | - | 0,02 | |
| б | 0,7 | 0,2 | 0,8 | 0,1 | ||||
| в | 0,2 | 0,6 | 0,5 | 2,5 | - | 0,02 | ||
| а | 1,4 | 1,4 | 0,8 | 0,78 | - | 0,03 | ||
| б | 0,7 | 0,2 | 0,4 | 1,8 | 0,05 | |||
| в | 0,4 | 0,2 | 1,6 | 0,8 | 3,2 | - | 0,05 | |
| а | 1,2 | 0,7 | 2,8 | 1,2 | 1,24 | - | 0,02 | |
| б | 1,2 | 0,5 | 0,5 | 0,4 | 1,8 | 0,05 | ||
| в | 0,2 | 0,5 | 1,6 | 0,8 | 3,2 | - | 0,05 | |
| а | 1,4 | 1,2 | 0,75 | 1,75 | - | 0,025 | ||
| б | 0,35 | 0,8 | 0,05 | |||||
| в | 0,4 | 0,4 | 0,3 | 1,2 | - | 0,02 | ||
| а | 1,6 | 0,4 | 3,4 | 2,5 | - | 0,02 | ||
| б | 0,5 | 0,5 | 0,5 | 0,05 | ||||
| в | 0,5 | 0,5 | 0,5 | - | 0,1 |
Для цифрової системи вірним буде вираз
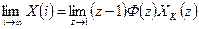 (3.1)
(3.1)
Тут
Ф(z) - z-передаточна функція цифрової системи;
Xз(z) - z-зображення вхідної величини.
Аналогічно можна знайти також усталену похибку
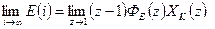 (3.2)
(3.2)
У виразі (3.2)
Е - різниця між заданим та дійсним значеннями керованої величини (похибка);
ФЕ(z) – z-передаточна функція замкнутої цифрової системи по похибці.
Якщо на вхід системи подавати одиничний ступінчастий сигнал
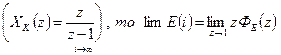 (3.3)
(3.3)
Отже, у цьому випадку усталену похибку можна визначити, якщо в z передаточну функцію цифрової системи по похибці ФЕ(z) замість z підставити 1.
Нагадуємо, що z-передаточну функцію ФЕ(z) можна знайти, маючи z-передаточну функцію розімкнутої цифрової системи,
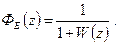
Z-передаточна функція одноконтурної цифрової системи дорівнює добутку з z-передаточних функцій регулятора D(z) та зведеної неперервної частини WПН(z)
W(z} = D(z}-WПН(z}. (3.4)
Тривалість перехідного процесу та його перерегулювання можна оцінити, маючи перехідну характеристику системи.
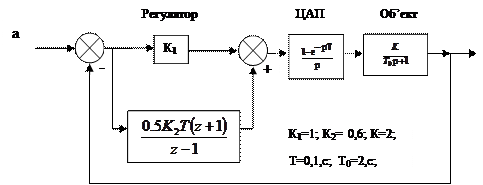
Приклад 3.1. Для цифрової системи, структурна схема якої задана на рис. 3.2а, знайти z-передаточну функцію WПН(z) зведеної неперервної частини. Скласти розрахункову структурну схему згідно з z-передаточними функціями цифрового регулятора та зведеної неперервної частини. Записати різницеві рівняння для регулятора та зведеної неперервної частини. Користуючись таблицями зворотного z-перетворення, знайти аналітичний вираз для розрахунку перехідної характеристики замкнутої системи. Визначити також усталену похибку при одиничному ступінчастому вхідному впливові. Записати також різницеве рівняння замкнутої системи.
Z-передаточна функція зведеної неперервної частини
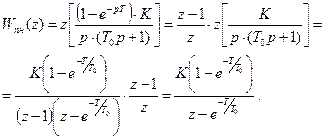
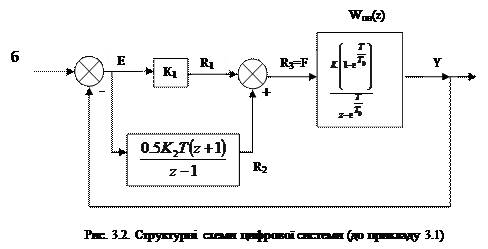
З урахуванням (3.5) складаємо розрахункову структурну схему системи (рис. 3.2, 6), згідно з якою запишемо різницеві рівняння елементів системи в z-формі:
для регулятора
R1(z} = K1E(z]
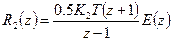 (3.6)
(3.6)
R3(z) = F(z) = Rl(z) + R2(z);
для зведеної неперервної частини
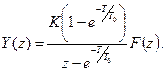 (3.7)
(3.7)
Переходимо тепер до різницевих рівнянь у часовій формі:
для регулятора
R1(n + l) = KlE(n + l)
R2(n + 1) = R2(n) + 0,5К2Т[Е(n + 1)-Е(n)] (3.8)
R3(n + l) = F(n + l) = R1(n + 1)+R2(n + l);
для зведеної неперервної частини
 |
 |
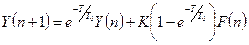 (3.9)
(3.9)
Згідно з рис. 3.2,б, враховуючи задані параметри, запишемо z-передаточні функції цифрового регулятора D(z) та зведеної неперервної частини Wзн (z)
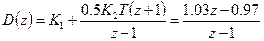 (3.10)
(3.10)
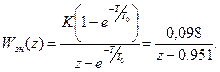
Z-передаточна функція розімкнутої системи
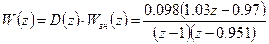 (3.11)
(3.11)
Z-передаточна функція замкнутої системи
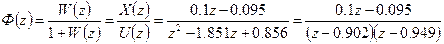 (3.12)
(3.12)
Z-передаточна функція системи за похибкою
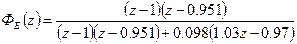
Підставивши в (3.13) z = l, визначаємо, що усталена похибка Еуст = 0.
При 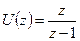 запишемо z-зображення керованої величини системи
запишемо z-зображення керованої величини системи
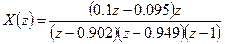 (3.14)
(3.14)
Скориставшись методом невизначених коефіцієнтів, вираз (3.14) можна записати так
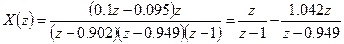
Згідно з таблицею зворотного z-перетворення записуємо аналітичний вираз для кривої перехідного процесу
Х(і) = 1(і)-1,042(0,902)і + 0,042(0,949)і. (3.16)
Маючи z-передаточну функцію Ф(z) замкнутої системи, можемо записати різницеве рівняння в z-формі
(z2-l,851z. + 0,856)Х(z) = (0,lz-0,095)U(z), (3.17)
або ж у часовій формі
Х(n + 2}-1,851Х(n + 1) + 0,856Х(n) = 0,1 U(n + 1)-0,095 U(n).
Для коефіцієнтів цього рівняння вводимо позначення
а0 = 0,856; а1 = -1,851; а2 = 1; b0 = -0,095; b1 = 0,1.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|