
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Метод замены переменной. Метод интегрирования по частям. Закрепление метода интегрирования по частям
5. Метод замены переменной
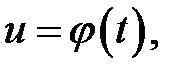 где
где  монотонная, непрерывна дифференцируемая функция новой переменной
монотонная, непрерывна дифференцируемая функция новой переменной 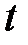 . Формула замены переменной в этом случае:
. Формула замены переменной в этом случае:
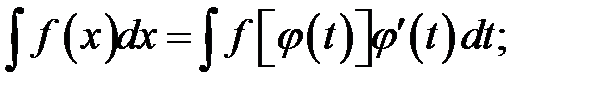 b)
b)  где
где 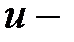 новая переменная. Формула замены переменной при такой подстановке:
новая переменная. Формула замены переменной при такой подстановке:
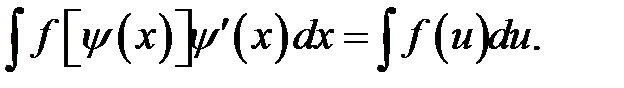
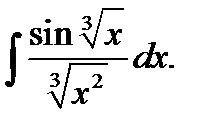 Какую сделаем замену?
Какую сделаем замену?
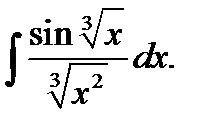 Сделаем замену
Сделаем замену 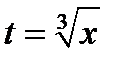 , т.е.
, т.е. 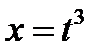 , тогда
, тогда 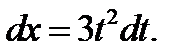 Отсюда получаем
Отсюда получаем
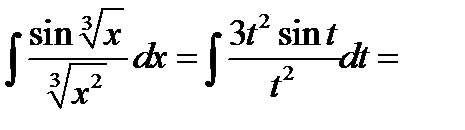
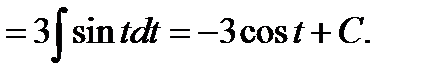 Вернемся к замене переменной
Вернемся к замене переменной
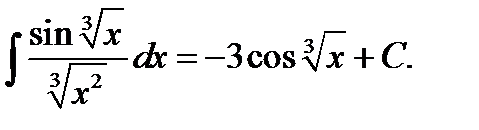 Ответ:
Ответ: 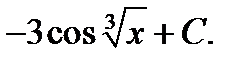
6. Метод интегрирования по частям
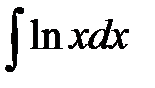 ;
;
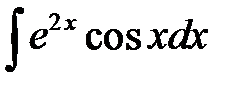 ;
;
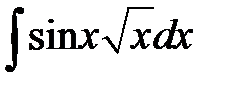 .
Такие интегралы мы не сможем посчитать только с помощью ранее изученных свойств и таблицы интегралов.
Для вычисления некоторых трансцендентных функций, а также произведений алгебраических и трансцендентных функций используется метод интегрирования по частям.
.
Такие интегралы мы не сможем посчитать только с помощью ранее изученных свойств и таблицы интегралов.
Для вычисления некоторых трансцендентных функций, а также произведений алгебраических и трансцендентных функций используется метод интегрирования по частям.
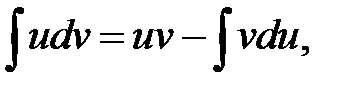 где
где 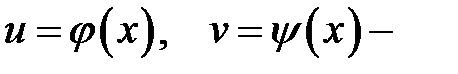 дифференцируемые функции.
дифференцируемые функции.
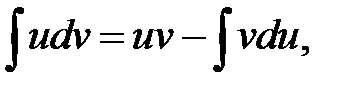 где
где 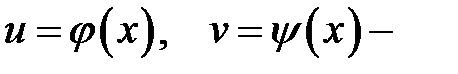 дифференцируемые функции.
дифференцируемые функции.
7. Закрепление метода интегрирования по частям
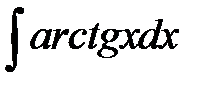 .
Пусть
.
Пусть 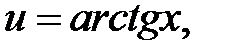
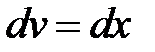 , тогда
, тогда 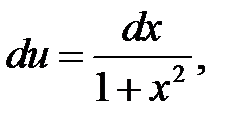
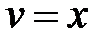 .
По формуле интегрирования по частям получим
.
По формуле интегрирования по частям получим
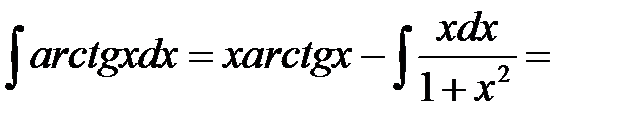


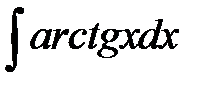 Пусть
Пусть 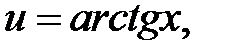
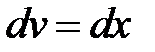 , тогда
, тогда 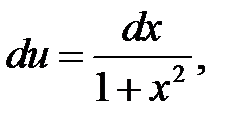
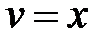 .
По формуле интегрирования по частям получим
.
По формуле интегрирования по частям получим
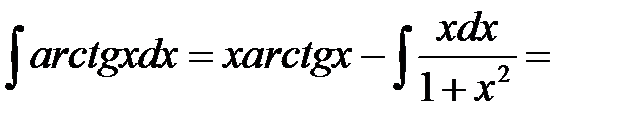


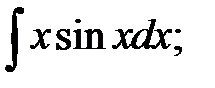 Что положим за
Что положим за 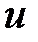 ? за
? за 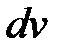 ? К какому интегралу сведется решение?
Если выбрать значения
? К какому интегралу сведется решение?
Если выбрать значения 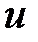 и
и 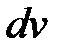 иначе, к какому интегралу сведется решение?
Итак, мы пришли к интегралу более сложному, чем исходный, так как степень сомножителя при тригонометрической функции повысилась на единицу.
Во многих случаях легко интегрируемые выражения, такие как
иначе, к какому интегралу сведется решение?
Итак, мы пришли к интегралу более сложному, чем исходный, так как степень сомножителя при тригонометрической функции повысилась на единицу.
Во многих случаях легко интегрируемые выражения, такие как 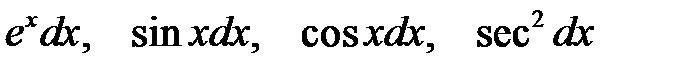 и т.д. рекомендуется принимать за
и т.д. рекомендуется принимать за 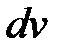 , а множитель при них принимать за
, а множитель при них принимать за 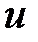 . Если же подынтегральное выражение содержит в качестве множителя такие функции как
. Если же подынтегральное выражение содержит в качестве множителя такие функции как 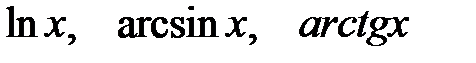 и т.д., интегралы от которых не являются табличными, то в большинстве случаев эти функции целесообразно принимать за
и т.д., интегралы от которых не являются табличными, то в большинстве случаев эти функции целесообразно принимать за 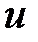 .
.
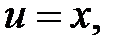
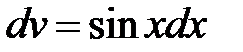 , тогда
, тогда 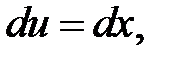
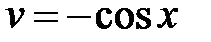 .
По формуле интегрирования по частям получим
.
По формуле интегрирования по частям получим
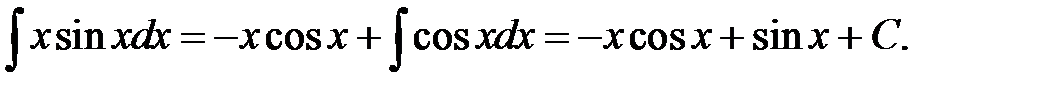 Выберем
Выберем 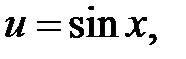
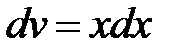 , тогда
, тогда 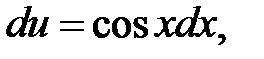
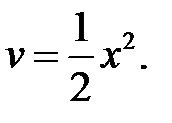 По формуле интегрирования по частям получим
По формуле интегрирования по частям получим
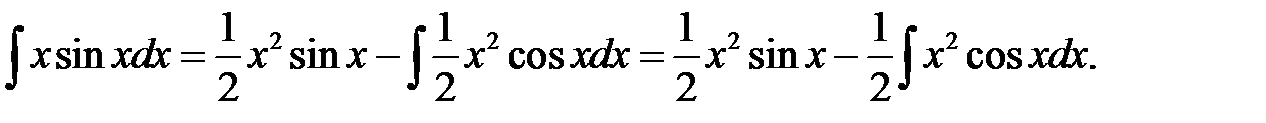 Ответ:
Ответ: 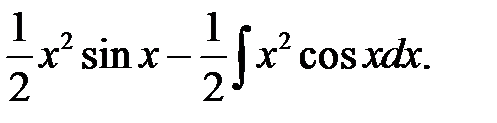
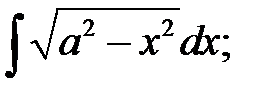 если
если 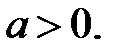 Что положим за
Что положим за 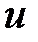 ? за
? за 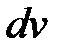 ? К какому интегралу сведется решение?
Если выбрать значения
? К какому интегралу сведется решение?
Если выбрать значения 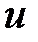 и
и 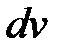 иначе, к какому интегралу сведется решение?
иначе, к какому интегралу сведется решение?
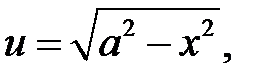
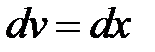 , тогда
, тогда 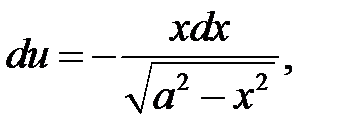
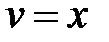 .
По формуле интегрирования по частям получим
.
По формуле интегрирования по частям получим
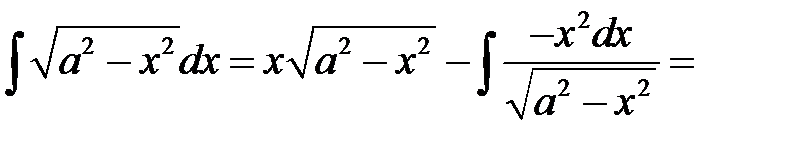
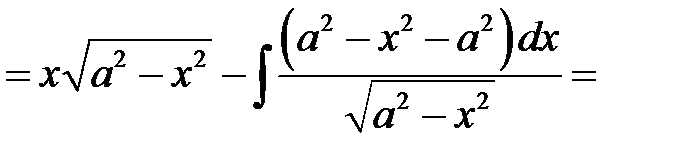
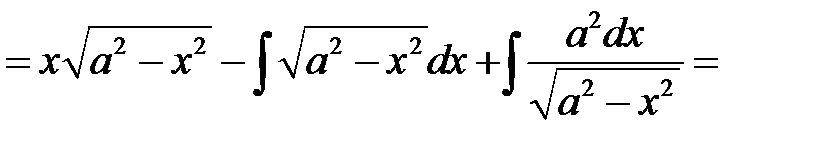
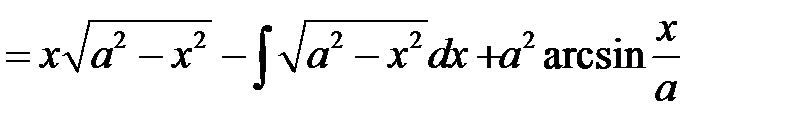 .
Отсюда получим
.
Отсюда получим
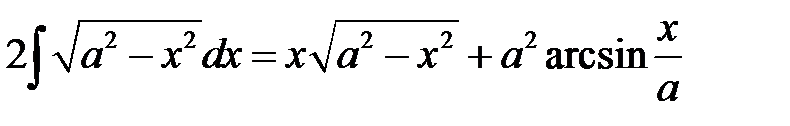 ;
;
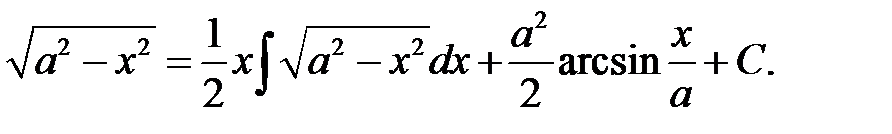 Ответ:
Ответ: 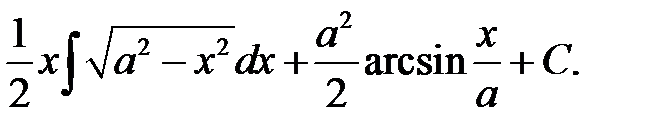
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|