
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Изложение нового материала
3. Изложение нового материала
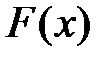 называется первообразной для функции
называется первообразной для функции 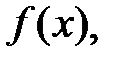 если
если 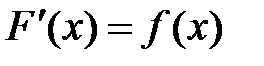 или
или 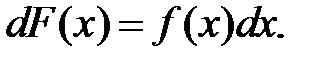
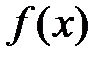 имеет первообразную
имеет первообразную 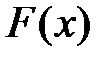 , то она имеет бесконечное множество первообразных, причем все первообразные содержатся в выражении
, то она имеет бесконечное множество первообразных, причем все первообразные содержатся в выражении 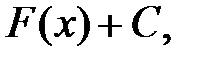
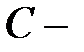 где постоянная.
Рассмотрим геометрический смысл первообразной, исходя из теоремы.
Посмотрите на рисунок. Как получаются графики всех первообразных для функции
где постоянная.
Рассмотрим геометрический смысл первообразной, исходя из теоремы.
Посмотрите на рисунок. Как получаются графики всех первообразных для функции 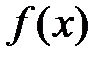 ? Сформулируйте геометрический смысл первообразной.
? Сформулируйте геометрический смысл первообразной.
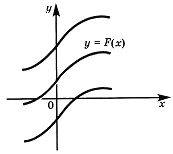
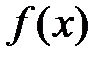 получаются из графика какой-либо одной первообразной параллельными переносами вдоль оси Оу.
получаются из графика какой-либо одной первообразной параллельными переносами вдоль оси Оу.
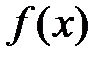 (или от выражения
(или от выражения 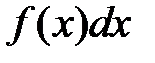 ) называется совокупность всех ее первообразных.
Обозначается
) называется совокупность всех ее первообразных.
Обозначается
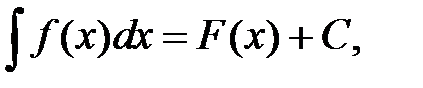 где
где 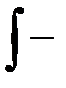 знак интеграла,
знак интеграла, 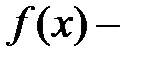 подынтегральная функция,
подынтегральная функция, 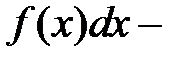 подынтегральное выражение,
подынтегральное выражение, 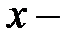 переменная интегрирования.
Символ
переменная интегрирования.
Символ 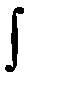 введен Лейбницем в 1675 г. Этот знак является изменением латинской буквы S.
Определение 3.Отыскание неопределенного интеграла называется интегрированием функции.
введен Лейбницем в 1675 г. Этот знак является изменением латинской буквы S.
Определение 3.Отыскание неопределенного интеграла называется интегрированием функции.
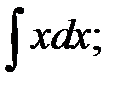 2.
2. 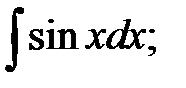 3.
3. 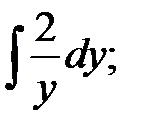 4.
4. 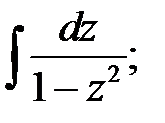
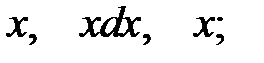 2.
2. 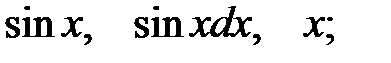 3.
3. 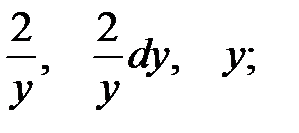 4.
4. 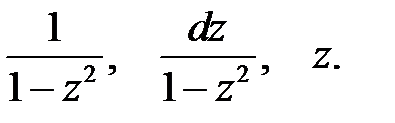
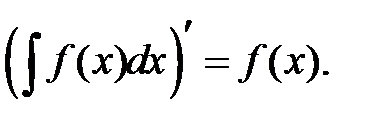 2.
2. 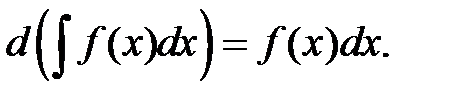 3.
3. 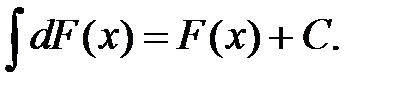 4.
4. 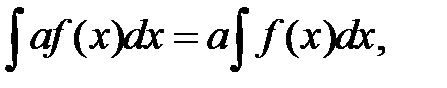 где
где 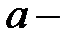 постоянная.
5.
постоянная.
5. 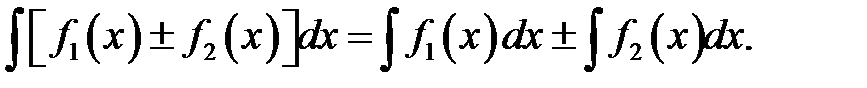 Если
Если 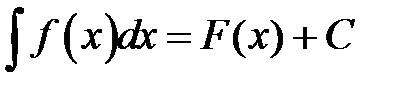 и
и 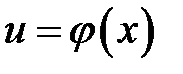 , то
, то 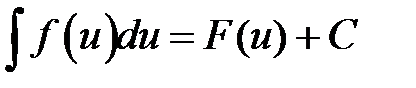 .
.
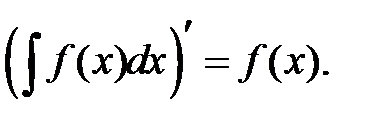
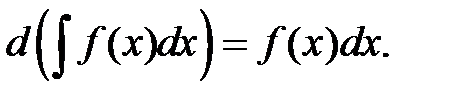
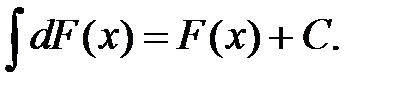
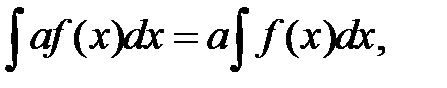 где
где 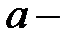 постоянная.
постоянная.
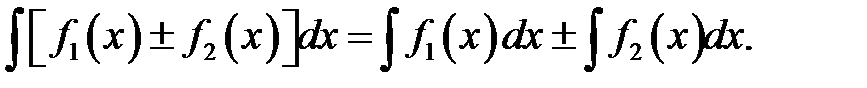 Если
Если 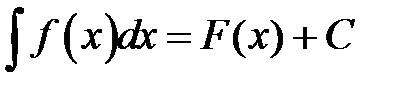 и
и 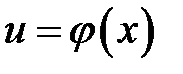 , то
, то 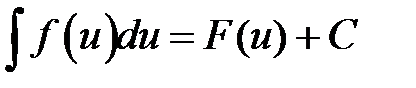 .
.
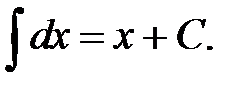 II.
II. 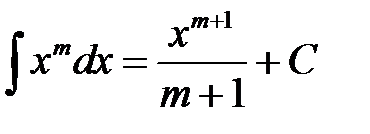 при
при 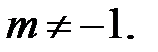 III.
III.  IV.
IV. 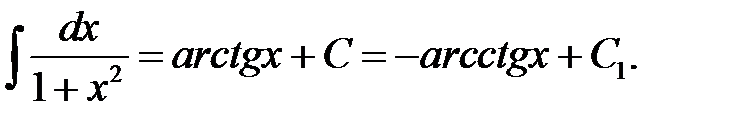 V.
V. 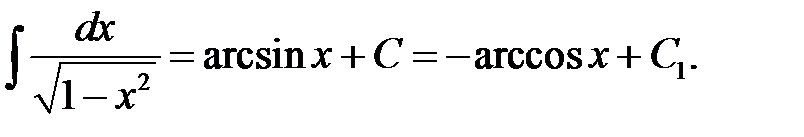 VI.
VI. 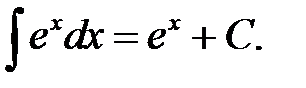 VII.
VII. 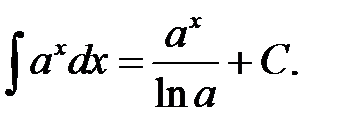 VIII.
VIII. 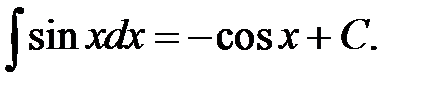 IX.
IX. 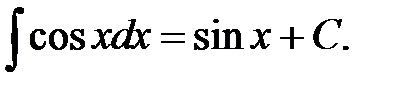 X.
X. 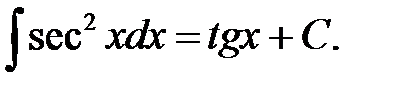 XI.
XI. 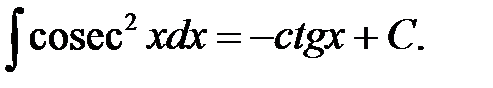 XII.
XII. 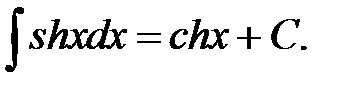 XIII.
XIII. 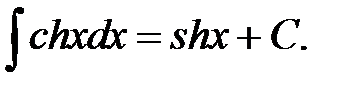 XIV.
XIV. 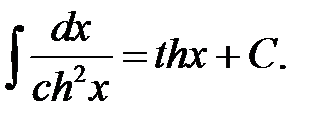 XV.
XV. 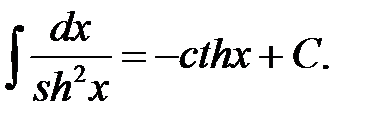 XVI.
XVI. 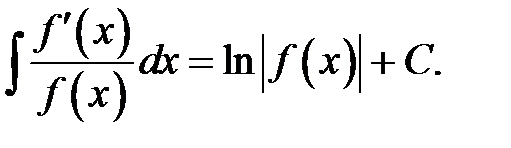 XVII.
XVII. 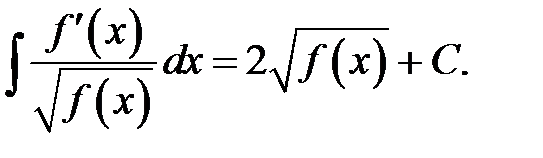 XVIII.
XVIII. 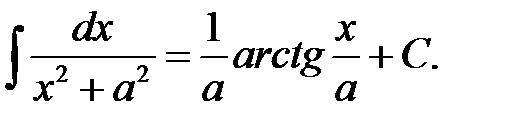 XIX.
XIX. 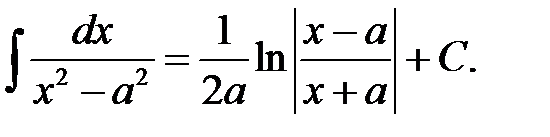 XX.
XX. 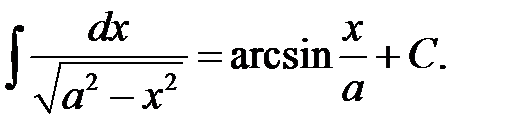 XXI.
XXI. 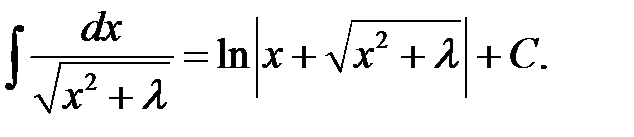 XXII.
XXII. 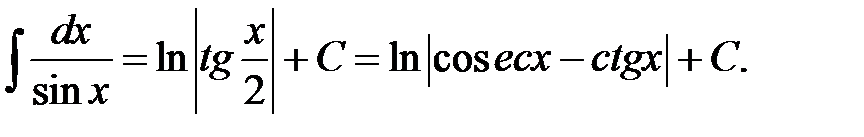 XXIII.
XXIII. 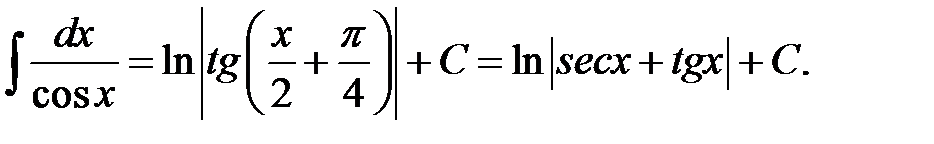 XXIV.
XXIV. 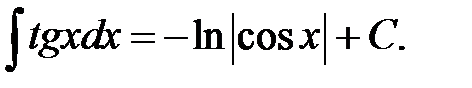
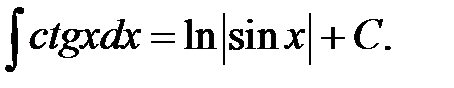
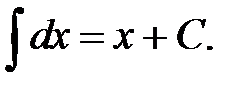 XXVI.
XXVI. 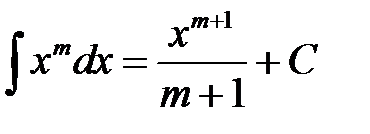 при
при 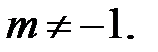 XXVII.
XXVII.  XXVIII.
XXVIII. 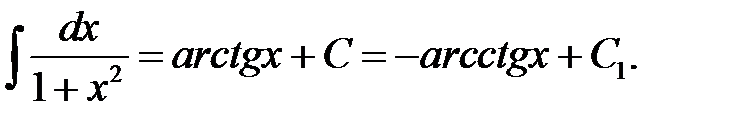 XXIX.
XXIX. 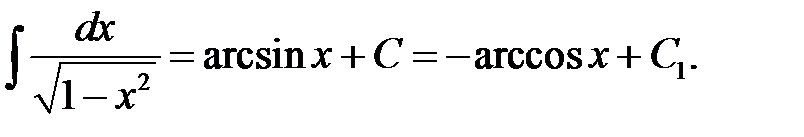 XXX.
XXX. 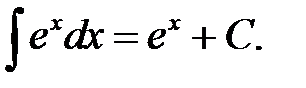 XXXI.
XXXI. 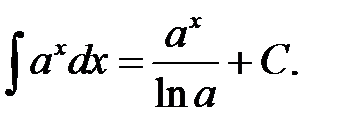 XXXII.
XXXII. 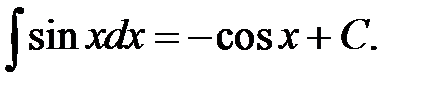 XXXIII.
XXXIII. 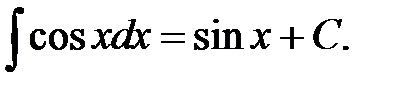 XXXIV.
XXXIV. 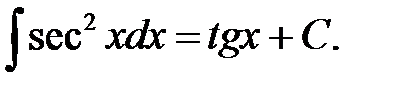 XXXV.
XXXV. 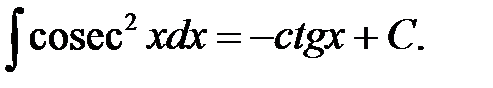 XXXVI.
XXXVI. 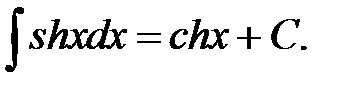 XXXVII.
XXXVII. 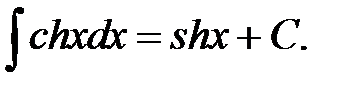 XXXVIII.
XXXVIII. 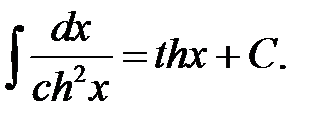 XXXIX.
XXXIX. 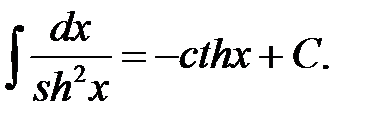 XL.
XL. 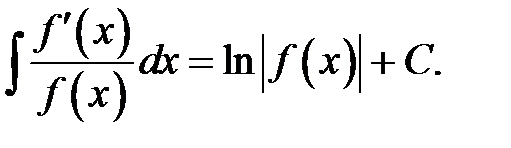 XLI.
XLI. 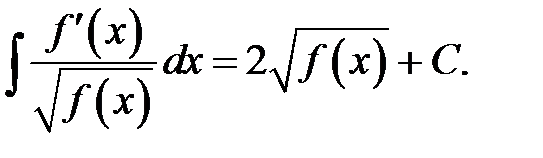 XLII.
XLII. 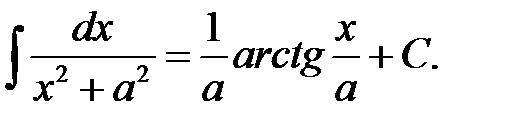 XLIII.
XLIII. 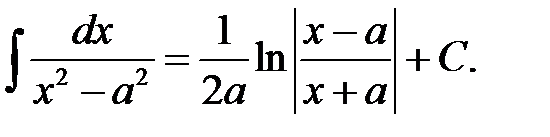 XLIV.
XLIV. 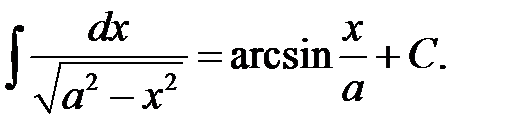 XLV.
XLV. 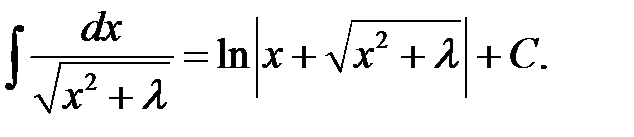 XLVI.
XLVI. 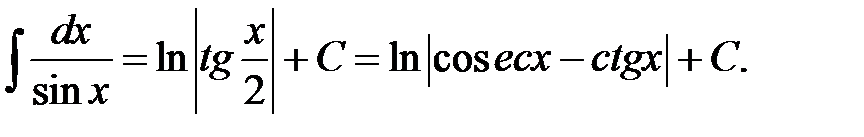 XLVII.
XLVII. 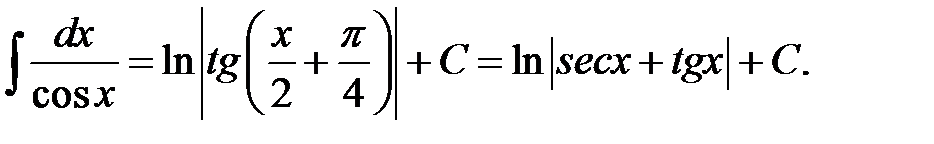 XLVIII.
XLVIII. 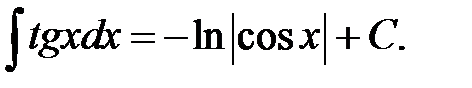 XLIX.
XLIX. 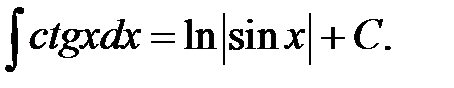
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|