
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Выпуклость графика функции. Точки перегиба.
Пример.
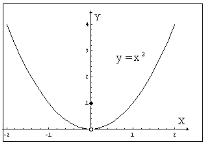 Исследовать на экстремум функцию
Исследовать на экстремум функцию 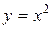 .
.
Решение.
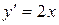 .Найдем критические точки:
.Найдем критические точки:
а) 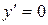 , если
, если 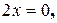 т.е.
т.е. 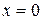 .
.
б). 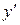 не существует – таких точек нет.
не существует – таких точек нет.
|
|
|
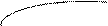

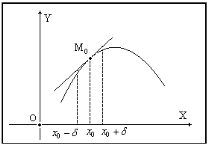
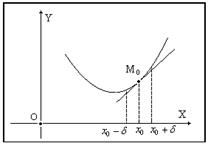
 Следовательно, имеем одну критическую точку
Следовательно, имеем одну критическую точку 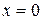 . Отметим на области определения функции эту точку и интервалы монотонности:
. Отметим на области определения функции эту точку и интервалы монотонности:
 |
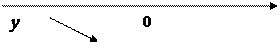 |
→ точка  является точкой локального минимума.
является точкой локального минимума.  , т.к. при
, т.к. при 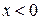 производная отрицательна и функция убывает, а при
производная отрицательна и функция убывает, а при 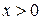 производная положительна и функция возрастает.
производная положительна и функция возрастает.
▲ Выпуклость графика функции. Точки перегиба.
Определение 4. Дифференцируемая на  функция
функция 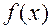
 называется выпуклой вверх (вниз), если ее график лежит ниже (выше) любой касательной.
называется выпуклой вверх (вниз), если ее график лежит ниже (выше) любой касательной.
При этом :
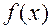 выпуклая вверх
выпуклая вверх
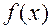 выпуклая вниз
выпуклая вниз
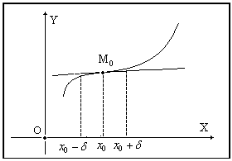
Определение 5.
Если справа и слева от т.  функция имеет разные направления выпуклости, то точка
функция имеет разные направления выпуклости, то точка  называется точкой перегиба (ТП).
называется точкой перегиба (ТП).
Например, на рисунке точка  − ТП.
− ТП.
Теорема 6. (Достаточный признак выпуклости- вогнутости)
Если 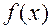 дважды дифференцируема на
дважды дифференцируема на 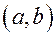 ,то:
,то:
· 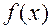 − выпуклая, если
− выпуклая, если 
· 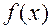 − вогнутая, если
− вогнутая, если 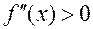
(Без доказательства).
Теорема 7. ( Необходимое условие т. перегиба (ТП).
Если 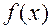 имеет перегиб в т.
имеет перегиб в т. 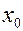 , то
, то 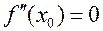 или
или 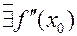
Доказательство. Очевидно (О1 и О2).
Теорема 8. ( Достаточное условие ТП.)
Если в т. 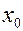
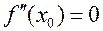 или
или 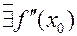 , а знаки
, а знаки 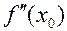 справа и слева т.
справа и слева т. 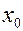 различны, то т.
различны, то т. 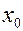
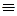 ТП.
ТП.
Доказательство. Очевидно по О2.
▲ Асимптоты графика функции
Определение 6. Если расстояние от точки, лежащей на кривой, до некоторой прямой стремится к нулю при неограниченном удалении этой точки от начала координат, то эта прямая называется асимптотой кривой. Асимптоты могут быть вертикальными, горизонтальными и наклонными.
Определение 7. Прямая 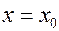 является вертикальной асимптотой графика функции
является вертикальной асимптотой графика функции  , если хотя бы один из пределов
, если хотя бы один из пределов 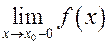 или
или 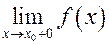 равен
равен 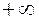 или
или  .
.
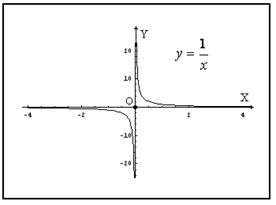 Пример: график функции
Пример: график функции 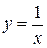 имеет вертикальную асимптоту
имеет вертикальную асимптоту  (в этой точке разрыв
(в этой точке разрыв  рода)
рода)
Замечание: непрерывные функции, очевидно, вертикальных асимптот не имеют! Асимптоты возможны только в точках разрыва функции.
Определение 8. Прямая 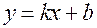 называется правой наклонной асимптотой графика функции
называется правой наклонной асимптотой графика функции  , если:
, если: 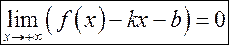 .
.
Аналогично определяетсялевая наклонная асимптота( 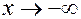 )
)
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|