Хелпикс

Главная

Контакты

Случайная статья



Экстремум функции

⇐ ПредыдущаяСтр 2 из 4Следующая ⇒


▲ Экстремум функции

Определение 2. Функция 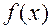 имеет в точке :
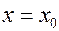─ локальный максимум (max), если существует такая окрестность т. 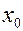: 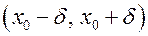, что для  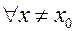из этой окрестности: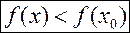
─ локальный минимум (min), если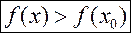

Локальные max и min называются локальными экстремумами.

Определение 3.  Точки, в которых 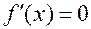 или 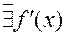 называются критическими. 

Точки, в которых 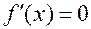 называются стационарными.

Экстремум может быть только в критических точках, но - критические точки лишь «подозрительны» на экстремум.

 

Пример.

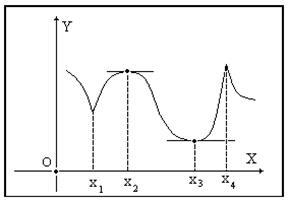
 На рисунке показано четыре экстремума в критических точках. Точк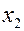и  

 и 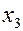 - стационарные.

В точках 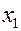 и  . .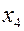

 

 

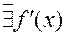Теорема 3. (Необходимое условие экстремума)
Если 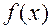 дифференцируема в т.  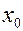и имеет в этой точке локальный экстремум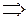

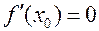
(без доказательства)

Замечание. Теорема 3 – необходимое, но не достаточное условие!

   

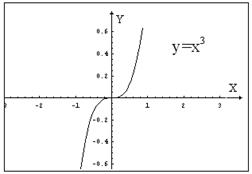
Пример: Для функции 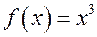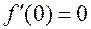, но экстремума в этой точке нет.

Теорема 4. (Достаточное условие экстремума)

Пусть 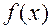 дифференцируема в некоторой окрестности критической т. 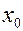, кроме, может быть, самой т. 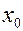. Тогда:

1. Если справа и слева от т. 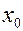 знак 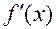одинаков - экстремума  в 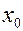т.  нет.

2. Если при переходе через т. 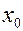 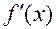меняет знак – в т.  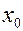есть локальный экстремум, причем характер экстремума определяется так:
если знак меняется с 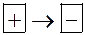 – это max

    с 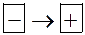 – это min.

Доказательство. Очевидно.

Теорема 5.  (Второе достаточное условие экстремума)

Пусть 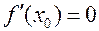  и 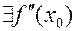. Тогда:

§ в т. 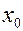 max , если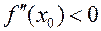

§ в т. 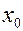 min , если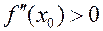

(Без доказательства.)


⇐ Предыдущая1234Следующая ⇒
  

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.