
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Постановка проблемы №2. Проблема №3. Постановка проблемы №3
Постановка проблемы №2
Таким образом представляется необходимым ввести функции N,n,p… (Количества молекул, концентрации, давления…) так, что бы они были бы дифференцируемыми функциями. (В том числе, в обобщенном смысле, о котором шла речь в пункте 1). И так, что бы уравнения МКТ не противоречили постулатам МКТ.
В рамках решения данной проблемы будет сформулирован математический аппарат исследования дискретных систем, состоящих из большого числа элементов. Этот аппарат будет удобно применять не только в рамках МКТ, но и в других областях физики.
Проблема №3
В физике очень часто приходится слышать фразу “заменим сумму на интеграл” при переходе от описания материальных точек к описанию непрерывных тел. Но проблема в том, что нет ни одного постулата, согласно которому это делается. А замена суммы на интеграл это не равносильный переход. Решительно не ясно, почему если мы можем что то ставить в соответствие системе точечных масс, то это же, только с заменной суммы на интеграл будет отвечать описанию непрерывного тела. Так же не ясно, что из себя представляет само по себе описание тела, как материальной точки. В действительности не существует точечных масс, ровно как и не существует математической формулировки того, как связанна модель материальной точки с моделью непрерывного тела.
Постановка проблемы №3
Представляется необходимым сформулировать математическую взаимосвязь между моделями материальной точки и непрерывного тела, показав, почему мы можем писать уравнения динамики для материальных точек, а потом пользуясь простым алгоритмом “заменим сумму на интеграл” получать описание непрерывного тела.
Решение проблемы №1.
Определение пространственного множества X
Множество X называется пространственным множеством, если все элементы множества принадлежат какому-либо пространству.
Под пространством понимается множество элементов для каждой пары которых определена функция расстояния.
Для любых элементов a,b,c 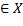 ,функция расстояния имеет свойства:
,функция расстояния имеет свойства:
1) 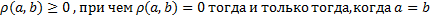
2) 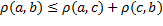
В дальнейшем, если не оговорено обратного, речь идет о пространственных множествах.
Если не оговорено обратного, имеется ввиду Евклидовое пространство.
(Для простоты понимая, имеет смысл представлять множество X, как просто множество геометрических точек)
Определение обобщенной функции
Обобщенной функцией 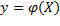 называется закон, ставящий в соответствие множеству X число (или вектор)
называется закон, ставящий в соответствие множеству X число (или вектор)  таким образом, что для любого разбиения множества X на подмножества
таким образом, что для любого разбиения множества X на подмножества 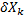 , такого что X=
, такого что X= 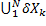 , всегда выполняется
, всегда выполняется 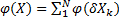 . (Что подразумевает, что
. (Что подразумевает, что 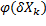 определенно для любого возможного элемента разбиения)
определенно для любого возможного элемента разбиения)
Определение предела обобщенной функции в точке
Выберем произвольную точку множества X. Зададим последовательность сужающихся объемов к этой точке. (То есть max(D) -максимальный диаметр объема стремится к нулю). Так, получим последовательность 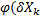 ). Если существует конечный предел
). Если существует конечный предел 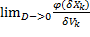 =
= 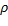 , при чем он не зависит от способа выбора сужающихся объемов, то число
, при чем он не зависит от способа выбора сужающихся объемов, то число 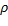 =
= 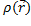 называется плотностью пространственного множества X в точке
называется плотностью пространственного множества X в точке 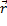 .
.
( 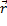 это просто способ указания элемента. Это радиус вектор, когда речь идет о геометрических множествах точек. О которых преимущественно и идет речь)
это просто способ указания элемента. Это радиус вектор, когда речь идет о геометрических множествах точек. О которых преимущественно и идет речь)
Определение бесконечно малой обобщенной функции в точке
Обобщенная функция o(V) множества X, называется бесконечно малой функцией в точке 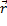 , по сравнению с V, если
, по сравнению с V, если 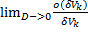 =0.
=0.
Теорема
Если 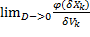 =
= 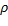 в точке
в точке 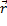 , то в этой точке верно разложение:
, то в этой точке верно разложение: 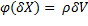 + o(δV)
+ o(δV)
Доказательство
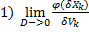 =
= 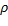
Рассмотрим обобщенную функцию: 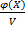 –
– 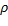
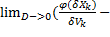
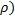 =
= 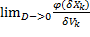 -
- 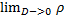 = 0
= 0
(Аддитивность предела очевидна и следует напрямую из определения, так как предел последовательности аддитивен)
Так, по определению: 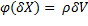 + o(δV)
+ o(δV)
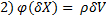 + o(δV)
+ o(δV)
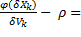 o(δV) =>
o(δV) => 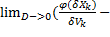
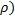 =0 =>
=0 => 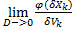 =
= 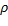
ч.т.д.
Определение
В равенстве 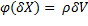 + o(δV), слагаемое
+ o(δV), слагаемое 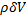 = f(
= f( 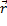 ,
, 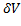 ) являющееся функцией 2-х переменных: вектора и скаляра, обозначим: d
) являющееся функцией 2-х переменных: вектора и скаляра, обозначим: d 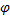 =
= 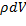 (dV
(dV 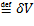 ) и назовем пространственным дифференциалом обобщенной функции
) и назовем пространственным дифференциалом обобщенной функции  .
.
Теорема
Если d 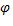 =
= 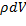 , то верно:
, то верно: 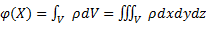
Доказательство
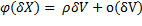
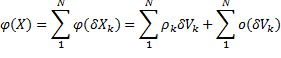
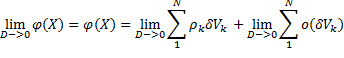
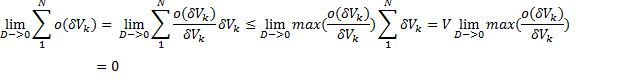
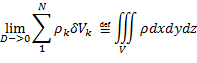
Последнее равенство является определение тройного интеграла, согласно “Второму тому по математическому анализу А.П. Аксенова”
Таким образом был определен математический объект, который в полной мере отвечает потребностям физики для использования дифференциального исчисления. В своей сущности это тоже самое, что было сформулировано для функции определенной на множестве чисел, только для функции определенной на множестве множеств.
Таким образом сразу становится ясно, что dm это в общем случае,это пространственный дифференциал обобщенной функции массы, являющейся мерой множества.
Ровно как и dI является пространственным дифференциалом обобщенной функции момента инерции.
Заметим, что функция m(x) массы стержня может быть рассмотрена, как обобщенная функция m(X), определенная на множестве точек стержня. Тогда dm(x)=dm(X) в точке x.
Решение проблемы №2.
Будем искать инструмент для анализа дискретных систем с большим количеством элементов. Основная проблема в том, что мы имеем куда больше информации, чем мы можем обработать. Даже если мы знаем координаты и импульсы молекул, мы попросту не сможем решить соответствующее количество уравнений движения. Алгоритм решения таких проблем следующий: Скажем, что дискретные элементы расположены случайным образом с некоторым законом распределения. И заменим их дискретные параметры (например количество штук, или количество ударов молекул, или что бы то ни было еще) соответствующими математическими ожиданиями.
В частности будем говорить не о количестве молекул в объеме 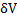 , а о математическом ожидании молекул в этом объеме. Обозначим это математическое ожидание N. Заметим это не числовая функция объема, как числа,
, а о математическом ожидании молекул в этом объеме. Обозначим это математическое ожидание N. Заметим это не числовая функция объема, как числа, 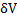 =2 литра например, а обобщенная функция N(
=2 литра например, а обобщенная функция N( 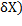 множества точек
множества точек 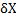 выбранного объема
выбранного объема 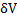 .
.
Концентрацию следует ввести, как n 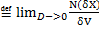 .
.
Тогда верно равенство: dN=ndV, как равенство в пространственных дифференциалах, функций (N и n) математического ожидания связанного с множеством дискретных элементов.
В любых задачах на дискретное моделирование создаются подобных объекты. И именно они и фигурируют в учебниках по физике. Только про это нигде не говорится. Интуиция физиков позволяет создавать какое-то не строгое представление об обобщениях и описывать мир, но тем не менее, представляется необходимым строгая формулировка действий.
В частности давление p= 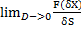 , где
, где 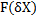 – обобщенная функция математического ожидания силы, действующая на плоское множество точек
– обобщенная функция математического ожидания силы, действующая на плоское множество точек 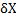 . Тогда мы сразу понимаем, что основное уравнение МКТ для 1 моля идеального газа pV=RT не противоречит постулатам теории, так как F=pS выражает собой не силу, а математическое ожидание силы. Что так же сразу проливает свет на то, почему мы это используем как силу и не задумываемся, ведь при огромном количестве молекул, для которых сила и математическое ожидание силы отождествимы в практических расчетах.
. Тогда мы сразу понимаем, что основное уравнение МКТ для 1 моля идеального газа pV=RT не противоречит постулатам теории, так как F=pS выражает собой не силу, а математическое ожидание силы. Что так же сразу проливает свет на то, почему мы это используем как силу и не задумываемся, ведь при огромном количестве молекул, для которых сила и математическое ожидание силы отождествимы в практических расчетах.
Что сразу показывает на границы применимости МКТ:
Границы применимости МКТ это границы, в которых математическое ожидание величин (например силы) можно отождествить с самой величиной (силой).
Решение проблемы №3.
Прежде всего необходимо отметить, что понятия массы и силы имеют смысл лишь в системе тезисов, описывающих их взаимные свойства. При чем эти тезисы сформулированы не для тел, а для материальных точек. Заметим, материальные точки, это не настоящие тела. Это отдельно созданные объекты, которые как-то характеризуют действительные тела. Они являются чем-то вроде “главной сути” тел по отношению к динамическому описанию при уменьшении самого тела. Подходящей аналогией является дифференциал функции, который является главной часть приращения, при малых приращениях аргумент.
Как уже было сказано, понятия массы и силы имеют лишь взаимный смысл, поэтому не имеет смысла пытаться разделить их определение на несколько частей. Все постулаты Ньютона и описание связи материальных точек (МТ) с действительными телами, должны быть сформулированы одним постулатом.
Механический Постулат:
Каждому физическому телу ставится в соответствие скаляр, называемый массой. Это характеристика задаваемая обобщенной функцией m(X), где X- множество точек тела, такая что, для нее выполняются соотношения приведенные ниже.
Каждой паре физических тел ставится в соответствие вектора 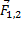 и
и 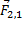 называемые силой действующей на первое тело, со стороны второго и силой действующей на второе тело, со стороны первого, соответственно.
называемые силой действующей на первое тело, со стороны второго и силой действующей на второе тело, со стороны первого, соответственно.
Каждому телу системы из N тел ставят в соответствие вектор 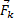 =
= 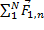 , называемый силой действующей на k-е тело со стороны других тел. Говорят так же “На тело действует сила”.
, называемый силой действующей на k-е тело со стороны других тел. Говорят так же “На тело действует сила”.
Заметим, что 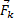 =
= 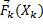 - обобщенная функция.
- обобщенная функция.
Если в системе только одно тело, то по определению говорят, что 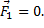
(Система это множество взаимодействующих тел)
Зададим отображение:
Выберем в каждом теле 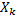 (в данном изложении k-е тело отождествляется с геометрическим множеством точек тела
(в данном изложении k-е тело отождествляется с геометрическим множеством точек тела 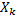 ) произвольную точку. Так получим множество из N точек. (По количеству тел в системе). Каждой такой точке поставим в соответствие m(
) произвольную точку. Так получим множество из N точек. (По количеству тел в системе). Каждой такой точке поставим в соответствие m( 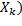 и
и 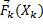 соответственно.
соответственно.
Такое отображение называется отображением множества действительных тел на множество материальных точек, а объекты, получаемые таким отображением, называются материальными точками.
Заметим, существует бесконечное число способов отобразить тело на пространство материальных точек.
По определению полагаем, что ускорение 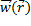 точек множества X действительного тела связана с ускорением материальной точки
точек множества X действительного тела связана с ускорением материальной точки 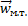 так, что:
так, что:
Если выбрать в теле последовательность сужающихся объемов к некоторой точке, то:
Для любого способа выбора отображения последовательности сужающихся объемов тела в пространство материальных точек и любого способа выбора геометрических точек тела, их ускорение 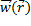 связанно с ускорение материальной точки
связанно с ускорение материальной точки 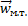 ,так что:
,так что:
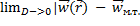 | = 0 и
| = 0 и 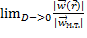 =1
=1
Можно переписать как: 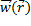 =
= 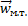 (
( 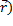 +
+ 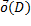
Постулируем, что существуют такие системы отсчёта, называемые инерциальными, относительно которых материальные точки, на которые не действует сила (то есть 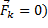 ,находятся в состоянии покоя или равномерного прямолинейного движения. (То есть
,находятся в состоянии покоя или равномерного прямолинейного движения. (То есть 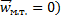
Постулируем, что в инерциальных системах отсчета ускорение материальной точки определяется соотношением: 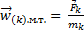 .
.
Постулируем что в инерциальных системах отсчета для любой пары тел: 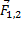 = -
= - 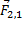
Смысл Механического Постулата:
Как не трудно видеть, в этом постулате сформулированы сразу 3 отдельных постулата Ньютона, но это необходимо делать в одном Постулате, так как только совокупность этих утверждений позволяет определить понятие массы и понятие силы.
В классической механике они сформулированы раздельно только потому, что классическая механика полагает интуитивно понятным понятие массы и силы, поэтому не требует их определения. Я полагаю, что необходимо формулировать эти 3 Постулата вместе, для определения взаимных свойств массы и силы, которые и задают эти понятия.
Ровно как нельзя сказать, что такое положительный заряд, не говоря о законе Кулона, так и нельзя сказать, что такое масса, не говоря о силе.
Попытка вести эти понятия независимо, заранее обречена на провал. Это полностью эквивалентно попытке поиска единственного решения уравнений x+y=2, x-y=4 независимо друг от друга.
О понятии материальной точки:
Как мы видим, МТ это такой объект, который выражает информацию о поступательном движении тела в тем большей мере, чем меньше диаметр рассматриваемого тела. Далее, можно утверждать, что: При уменьшении диаметра, угловая скорость вращения постоянна (мы рассматриваем тело в один и тот же момент времени), в то время как линейная скорость точек тела, полученная за счет его вращения стремится к нулю. Поэтому остается только поступательная часть движения. Поэтому можно сказать, что материальная точка выражает главную часть движения тела.
Пример рассуждения. Определение центра масс.
Разобьем тело X на подмножества 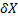 произвольным образом. И отобразим произвольным образом множество множеств
произвольным образом. И отобразим произвольным образом множество множеств 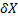 на пространство МТ.
на пространство МТ.
Получим: 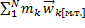 =
= 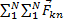 =
= 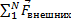 =
= 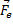
Сразу заменим на интеграл: 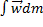 =
= 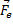
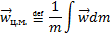
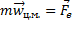
Распишем полностью, что мы сделали:
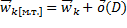
: 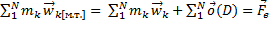
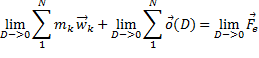
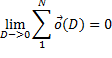
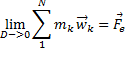
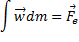
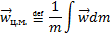
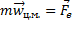
Таким образом, как мы видим, создание пространства МТ, позволяет довольно быстро и наглядно создавать аналитическое описание тел.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|