Проблема №1

Проблема №1

Пример №1 Рассмотрим жесткий стержень переменной плотности. Найдем его массу. Выделим бесконечно малый элемент этого стрежня длиной dx. Его масса dm = 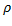dx. Далее “Объединяем” все элементарные массы интегрированием, получаем m = .

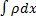Требование математической строгости вынуждает объяснить, чем является каждый объект уравнения. В частности: dm= 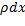. Что такое dm, которое мы назвали бесконечно малой массой?

1) “dm” не может быть числом, так как:

Для любого конечного объема, в общем случае масса не выражается dm= 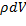.А понятие бесконечно малого числа, в математическом анализе, отсутствует в силу аксиомы Архимеда.

2) “dm” это дифференциал функции m(x)

Действительно, введя координату x по длине стержня, мы однозначно зададим функцию m(x). Разобравшись с классом объекта “dm” становится понятно, почему мы его назвали “бесконечно малой массой”. Современная математика отказалась от идей Лейбница об “актуальных бесконечно малых” и использует подход Коши “потенциально бесконечно малых”. То есть мы не говорим, что есть настоящее бесконечно малое число равное приращению функции, но говорим, что существует функция и ее дифференциал, он таков что, df тем больше является 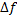, чем меньше 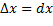. Само название “бес конечно” указывает на то, что наш разум не может себе вообразить бесконечность, а может лишь осознать отсутствие конца. Как мы не можем назвать максимальное число, но можем понять, что человек может называть числа все больше и больше, пока мы его не остановим. Поэтому мы и называем dm бесконечно малой массой, имея тем самым ввиду, что dm тем больше является 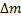выделенной длины, чем меньше .

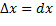И тогда сразу становится ясно, почему мы получаем исходную массу, как интеграл. И почему мы это можем называть суммой элементарных приращений. Потому что математически известна связь между f и df. С другой стороны 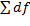тем больше является искомым числом, (суммарным приращением) чем меньше каждое приращение dx. И мы называем это “бесконечной суммой” имея тем самым ввиду, что чем больше в ней слагаемых (формально, чем меньше max(dx)), тем ближе мы к правильному ответу. А интеграл, это просто математический оператор, позволяющий нам получить ответ, который мы лирически можем считать суммой бесконечного числа слагаемых. Повторюсь, это только способ названия, ни о какой сумме и реально бесконечного числа слагаемых речи не идет.

Пример №2: Рассмотрим задачу: необходимо определить массу 3-мерного тела переменной плотности. Рассмотрим бесконечно малый объем исследуемого тела: бесконечно малая масса этого элементарного объема dm= 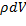. Далее “Объединяем” все элементарные массы интегрированием, получаем m = .

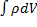Требование математической строгости вынуждает объяснить, чем является каждый объект уравнения. В частности: dm= 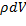. Что такое dm, которое мы назвали бесконечно малой массой?

1)“dm” не может быть числом, так как:

Для любого конечного объема, в общем случае масса не выражается dm= 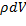.А понятие бесконечно малого числа, в математическом анализе, отсутствует в силу аксиомы Архимеда.

2)“dm” НЕ может быть дифференциалом функции m(V)

так как функции m(V) не существует. Действительно, мы не можем сказать массу части тела, зная лишь ее объем, необходимо так же знать и способ выбора данного объема. (В случае тела переменной плотности).

Пример №3:

Аналогично можно поступить при попытке определить момент инерции твердого тела относительно заданной оси. Сказав, что dI= 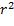dm, но и тут, как в предыдущем пункте, это не число и не дифференциал функции I(m), так как момент инерции это число отвечающее массе И способу расположения массы. Зная только массу, определить момент инерции невозможно.

⇐ Предыдущая 123 4 Следующая ⇒