Таблица 5. Рис.6. График остатков.

= = 0,581;

= = 0,339.

Где S²_x1= 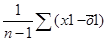² = 29,475; S_x1= 5,429;

S2x2= 2 = 76526,820; Sx2 = 276,635;

S2y= 2 = 0,824; Sу = 0,908.

Бета-коэфициент показывает, на какую часть величины среднего квадратического отклонения S_y изменится зависимая переменная Y с изменением соответствующей независимой переменой X _j на величину своего среднеквадратического отклонения при фиксированном на постоянном уровне значении остальных независимых переменных.

Т.е. если объем выполненных работ увеличится на 5,429 млн. руб., то величина накладных расходов увеличится на 0,581*0,908 = 0,528млн. руб.

Также, если численность рабочих увеличится на 277 чел., то величина накладных расходов увеличится на 0,339*0,908 = 0,308 млн. руб.

Долю влияния фактора в суммарном влиянии всех факторов можно оценить по величине дельта-коэфициентов 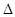_j_.

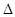_j = r _yx * ( 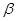/ R²)

Где r _yx - коэффициент парной корреляции между фактором X_j и зависимой переменой.

Получаем 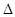_j = 0,851*(0,581/0,724) = 0,683, т.е. доля влияния объема выполненных работ на величину накладных расходов 68,3%.

Далее получаем 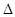_j = 0,851*(0,339/0,724) = 0,398, т.е. доля влияния численности рабочих на величину накладных расходов 39,8%.

Проверим выполнение предпосылок МНК.

По данным таблицы 5 построим график остатков(Рис.6).

Таблица 5

Наблюдение	Предсказанное Y	Остатки
	3,411347559	0,088652441
	3,091531483	0,908468517
	3,387817114	-0,287817114
	2,780562647	-0,080562647
	2,856897014	0,743102986
	2,848817721	-0,148817721
	2,675601722	0,224398278
	1,742886116	-0,142886116
	2,016320643	-0,716320643
	2,409650718	0,090349282
	2,307207593	-0,207207593
	2,289178128	0,110821872
	2,363055208	-0,363055208
	2,691588131	-0,191588131
	1,971070121	-0,171070121
	3,229465861	-0,429465861
	4,561691862	-0,561691862
	4,839017268	-0,939017268
	4,242076055	0,457923945
	3,7738589	1,0261411
	3,778843351	0,521156649
	3,666915432	-0,166915432
	3,47349652	-0,47349652
	3,576586564	0,023413436
	3,298218736	0,001781264
	3,398739831	-0,498739831
	3,29763233	-0,19763233
	3,646489193	-0,846489193
	3,118105621	0,381894379
	3,684963625	0,915036375
	2,800411844	0,699588156
	2,919306756	-0,019306756
	2,828856861	-0,128856861
	2,763524453	0,036475547
	2,577607791	0,422392209
	2,394716094	0,505283906
	2,136276705	0,263723295
	2,060863732	-0,460863732
	1,558891485	-0,358891485
	1,529911211	-0,029911211

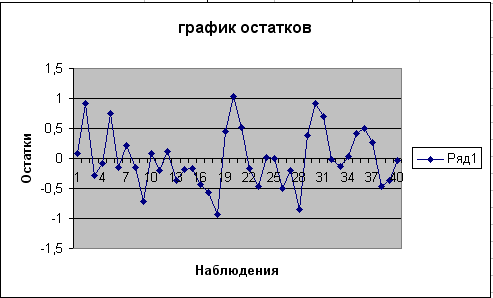
Рис.6. График остатков.

По графику видно, что остатки случайны. Грубых отклонений нет.

Проверим независимость остатков с помощью критерия Дарбина – Уотсона. Численное значение коэффициента равно (расчеты приведены в таблице 6).

dw = 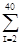( 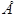_i- 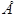_i_-1)² /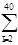 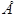_i²= 12,904/8,851 = 1,458

критические границы для dw: d₁ = 1,39; d₂ = 1,6 (Данные взяты из книги Доугерти К. «Введение в эконометрику», стр. 372). Так как d₁ < dw < d₂, то ситуация осталась неопределенной, применим другой критерий.

Для определения степени автокорреляции вычислим коэффициент автокорреляции и проверим его значимость при помощи критерия стандартной ошибки.

r(1) = 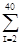( 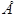_I * 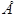_i_-1)² /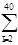 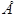_i²= 2.394/8.851 = 0.271

Стандартная ошибка коэффициента корреляции рассчитывается следующим образом. S_E= 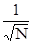= 1/40 = 0.158

Если r(1) находится в интервале -1,96*0,158 ≤ r ≤ 1,96*0,158, то можно считать, что данные не показывают наличие автокорреляции первого порядка, т.к. -0,310 ≤ r = 0,271 ≤ 0,310, то свойство независимости остатков выполняется.

⇐ Предыдущая 1 2 345 Следующая ⇒