Урок: Умножение и деление алгебраических дробей. Возведение дроби в степень

Урок: Умножение и деление алгебраических дробей. Возведение дроби в степень

1. Правила умножения обыкновенных и алгебраических дробей

Правила умножения и деления алгебраических дробей абсолютно аналогичны правилам умножения и деления обыкновенных дробей. Напомним их:

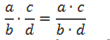
То есть, для того, чтобы умножить дроби, необходимо умножить их числители (это будет числитель произведения), и умножить их знаменатели (это будет знаменатель произведения).

2. Частные случаи применения правила умножения дробей

Несмотря на простоту данных правил, многие при решении примеров по данной теме допускают ошибки в ряде частных случаев. Рассмотрим подробнее эти частные случаи:

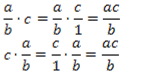
Во всех этих правилах мы пользовались следующим фактом: .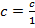

3. Примеры умножения алгебраических дробей

Рассмотрим умножение и деление алгебраических дробей.

Пример 1

Отметим, что сокращать дроби после умножения можно и даже нужно по тем же правилам, которые мы до этого рассматривали на уроках, посвящённых сокращению алгебраических дробей. Рассмотрим несколько простых примеров на частные случаи.

Пример 2

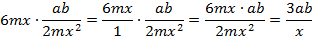
Пример 3

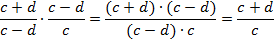
Пример 4

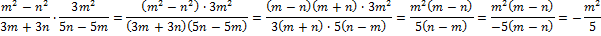
Правила возведения дробей и целых выражений в натуральную степень

Правило возведения обыкновенных и алгебраических дробей в натуральную степень:

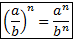
Можно провести аналогию со степенью целого выражения и вспомнить, что понимается под возведением его в степень:

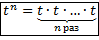
Пример 5. .

Как видно из примера, возведение дроби в степень – это частный случай умножения дробей, что изучалось на предыдущем уроке.

Пример 6. а) 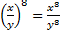, б) – минус уходит, т. к. мы возвели выражение в четную степень.

Ответ. ; .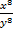

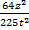Для удобства работы со степенями вспомним основные правила возведения в натуральную степень:

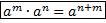– произведение степеней;

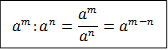– деление степеней;

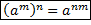– возведение степени в степень;

– степень произведения.

Пример 7. 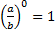– это известно нам еще с темы «Возведение в степень целых выражений», кроме одного случая: 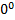не существует.

Простейшие примеры на возведение алгебраических дробей в натуральную степень

Далее рассмотрим примеры посложнее.

Пример 8. Возвести дробь в степень .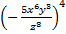

Решение. При возведении в четную степень минус уходит:

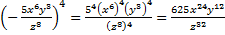Ответ. .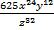

Пример 9. Возвести дробь в степень .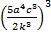

Решение. Теперь пользуемся правилами возведения степени в степень сразу без отдельного расписывания:

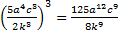Ответ. .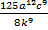

Теперь рассмотрим комбинированные задачи, в которых нам будет необходимо и возводить дроби в степень, и умножать их, и делить.

Пример 10. Выполнить действия .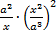

Решение. 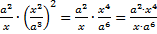. Далее необходимо произвести сокращение. Распишем один раз подробно, как мы это будем делать, а затем будем указывать результат сразу по аналогии: 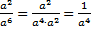. Аналогично (или по правилу деления степеней) 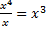. Имеем: .

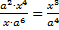Ответ. .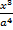

Пример 11. Выполнить действия .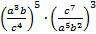

Решение. 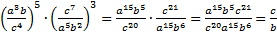. Сокращение осуществлено по аналогии с примером, разобранным ранее.

Ответ. .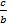

Пример 12. Выполнить действия .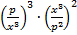

Решение. 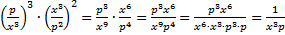. В данном примере мы еще раз более подробно расписали процесс сокращения степеней в дробях, чтобы закрепить этот способ.

Ответ. .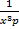

Более сложные примеры на возведение алгебраических дробей в натуральную степень (с учетом знаков и со слагаемыми в скобках)

Пример 13. Выполнить действия .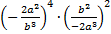

Решение. В данном примере уже пропустим отдельное умножение дробей, а сразу воспользуемся правилом их умножения и запишем под один знаменатель. При этом следим за знаками – в указанном случае дроби возводятся в четные степени, поэтому минусы исчезают. В конце выполним сокращение.

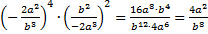Ответ. .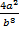

На данном уроке мы рассмотрели правила умножения алгебраических дробей, возведение дробей в натуральную степень, а также применение этих правил для конкретных примеров. В дальнейшем умение осуществлять действия с дробями, мы будем использовать для преобразования рациональных выражений.

12 3 4 5 6 7 8 9 10 Следующая ⇒