
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Примеры решения задач
Примеры решения задач
Пример 1. Первоначальная масса радиоактивного изотопа радона 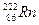 (период полураспада
(период полураспада 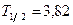 сут) равна 1,5 г. Определить: 1) начальную активность изотопа; 2) его активность через 5 сут.
сут) равна 1,5 г. Определить: 1) начальную активность изотопа; 2) его активность через 5 сут.
Решение. Начальная активность изотопа
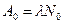 ,
,
где 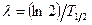 — постоянная радиоактивного распада;
— постоянная радиоактивного распада; 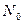 - число ядер изотопа в начальный момент времени:
- число ядер изотопа в начальный момент времени: 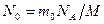 , где
, где 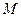 — молярная масса радона (
— молярная масса радона ( 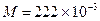 кг/моль);
кг/моль); 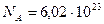 моль-1 постоянная Авогадро. Учитывая эти выражения, найдем искомую начальную активность изотопа:
моль-1 постоянная Авогадро. Учитывая эти выражения, найдем искомую начальную активность изотопа:
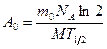 .
.
Активность изотопа 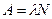 , где, согласно закону радиоактивного распада,
, где, согласно закону радиоактивного распада, 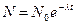 — число нераспавшихся ядер в момент времени t. Учитывая, что
— число нераспавшихся ядер в момент времени t. Учитывая, что 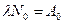 , найдём, что активность нуклида уменьшается со временем по закону
, найдём, что активность нуклида уменьшается со временем по закону
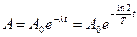 .
.
Вычисляя, получаем: 1) 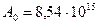 Бк; 2)
Бк; 2) 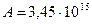 Бк.
Бк.
Пример 2. Вычислить дефект массы и энергию связи ядра 73Li.
Р е ш е н и е. Масса ядра всегда меньше суммы масс свободных (находящихся вне ядра) протонов и нейтронов, из которых ядро образовалось. Дефект массы ядра Δm и есть разность между суммой масс свободных нуклонов (протонов и нейтронов) и массой ядра, т. е.
Δm = Zmp + (A - Z)mn – mя, (1)
где Z – атомный номер (число протонов в ядре); А – массовое число (число нуклонов, составляющих ядро); mp, mn, mя – соответственно массы протона, нейтрона и ядра.
В справочных таблицах всегда даются массы нейтральных атомов, но не ядер, поэтому формула (1) целесообразно преобразовать так, чтобы в нее входила масса mя нейтрального атома. Можно считать, что масса нейтрального атома равна сумме масс ядра и электронов, составляющих электронную оболочку атома: mа = mя + Z mе, откуда
mя = mа - Z mе. (2)
Выразив в равенстве (1) массу ядра по формуле (2), получаем
Δ m = Z mp + (A – Z) mn – ma + Z me, или
Δ m = Z (mp + me) + (A - Z) mn – ma.
Замечая, что mр + mе = mн, где mн – масса атома водорода, окончательно находим
Δ m = Z mH + (A - Z) mn – ma.. (3)
Подставив в выражение (3) числовые значения масс, получим
Δm = [3 Ì 1,00783 + (7 - 3) Ì 1,00867 – 7 Ì 0,1601] а. е. м =0,04216 а. е. м.
В соответствии с законом пропорциональности масс и энергии
E = c2Δm, (4)
где с – скорость света в вакууме.
Коэффициент пропорциональности c2 может быть выражен двояко:
c2 = 9 Ì 1016 м2/с2, или c2 = ΔЕ/Δm = 9 Ì 1016 Дж/кг.
Если вычислить энергию связи, пользуясь внесистемными единицами, то c2 = 931 МэВ/а. е. м. С учетом этого формула (4) примет вид
Е = 931Δm (МэВ). (5)
Подставив найденное значение дефекта массы ядра в формулу (5), получим
Е = 931 Ì 0,04216 МэВ.
Пример 3.При соударении α-частицы с ядром бора 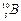 произошла ядерная реакция, в результате которой образовалось два новых ядра. Одним из этих ядер было ядро атома водорода 11Н. Определить порядковый номер и массовое число второго ядра, дать символическую запись ядерной реакции и определить ее энергетический эффект.
произошла ядерная реакция, в результате которой образовалось два новых ядра. Одним из этих ядер было ядро атома водорода 11Н. Определить порядковый номер и массовое число второго ядра, дать символическую запись ядерной реакции и определить ее энергетический эффект.
Р е ш е н и е. Обозначим неизвестное ядро символом AZX. Так как α-частица представляет собой ядро гелия 42Не, запись реакции примет вид
42Не + 105В → 11Н + AZX.
Применив закон сохранения числа нуклонов, получим уравнение 4 + 10 = 1+А, откуда А = 13. Применив закон сохранения заряда, получим уравнение 2 + 5 = 1 + Z, откуда Z =6. Следовательно, неизвестное ядро является ядром атома изотопа углерода 136С.
Теперь можно записать реакцию в окончательном виде:
42Не + 105В →11Н + 136С.
Энергетический эффект Q ядерной реакции определяется по формуле
Q = 931[(mHe + mB) – (mH + mC)].
Здесь в первых круглых скобках указаны массы исходных ядер, во вторых скобках – массы ядер – продуктов реакции. При числовых подсчетах по этой формуле массы ядер заменяют массами нейтральных атомов. Возможность такой замены вытекает из следующих соображений.
Число электронов в электронной оболочке нейтрального атома равно его зарядовому числу Z. Сумма зарядовых чисел исходных ядер равна сумме зарядовых чисел ядер – продуктов реакции. Следовательно, электронные оболочки ядер гелия и бора содержат вместе столько же электронов, сколько их содержат электронные оболочки ядер углерода и водорода.
Очевидно, что при вычитании суммы масс нейтральных атомов углерода и водорода из суммы масс атомов гелия и бора массы электронов выпадут и мы получим тот результат, как если бы брали массы ядер. Подставив массы атомов в расчетную формулу, получим
Q = 931(4,00260 + 10,01294) – (1,00783 + 13,00335) МэВ = 4,06 МэВ.
Пример 4.Удельная проводимость кремниевого образца при нагревании от температуры 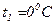 до температуры
до температуры 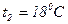 увеличилась в 4,24 раза. Определить ширину запрещенной зоны кремния.
увеличилась в 4,24 раза. Определить ширину запрещенной зоны кремния.
Решение. Удельная проводимость собственных полупроводников
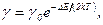
где 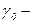 постоянная, характерная для данного полупроводника;
постоянная, характерная для данного полупроводника; 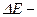 ширина запрещенной зоны.
ширина запрещенной зоны.
Тогда
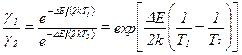 ,
,
или, прологарифмировав,
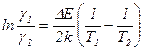 ,
,
откуда искомая ширина запрещенной зоны
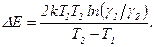
Вычисляя, получим 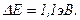
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|