
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Примеры решения задач
Примеры решения задач
Пример 1. Определить частоту света, излучаемого возбужденным атомом водорода, при переходе электрона на второй энергетический уровень, если радиус орбиты электрона изменился в 9 раз.
Решение. Согласно обобщенной формуле Бальмера, частота света, излучаемого атомом водорода,
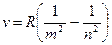 , (1)
, (1)
где 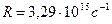 — постоянная Ридберга; m определяет серию (по условию задачи, m=2-серия Бальмера), т.е. номер орбиты, на которую переходит электрон; n определяет отдельную линию серии, т.е. номер орбиты, с которой переходит электрон.
— постоянная Ридберга; m определяет серию (по условию задачи, m=2-серия Бальмера), т.е. номер орбиты, на которую переходит электрон; n определяет отдельную линию серии, т.е. номер орбиты, с которой переходит электрон.
Второй закон Ньютона для электрона, движущегося по окружности радиусом 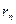 под действием кулоновской силы,
под действием кулоновской силы,
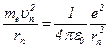 . (2)
. (2)
Согласно теории Бора, момент импульса электрона, движущегося по n-й орбите,
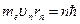
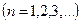 . (3)
. (3)
Решая уравнения (2) и (3), получим
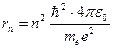 . (4)
. (4)
Из выражения (4) и условия задачи следует, что
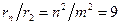 . (5)
. (5)
Умножив и разделив правую часть уравнения (1) на 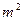 и учитывая (5), получим искомую частоту
и учитывая (5), получим искомую частоту
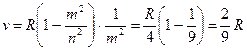 .
.
Вычисляя, получаем 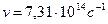 .
.
Пример 2. Электрон, начальной скоростью которого можно пренебречь, прошел ускоряющую разность потенциалов U. Найти длину волны де Бройля электрона для двух случаев: 1) 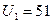 В; 2)
В; 2) 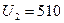 кВ.
кВ.
Решение. Длина волны де Бройля для частицы зависит от ее импульса ρ и определяется формулой
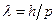 , (1)
, (1)
где h— постоянная Планка.
Импульс частицы можно определить, если известна ее кинетическая энергия Т. Связь импульса с кинетической энергией различна для нерелятивистского случая (когда кинетическая энергия частицы много меньше ее энергии покоя) и для релятивистского случая (когда кинетическая энергия сравнима с энергией покоя частицы).
В нерелятивистском случае
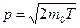 , (2)
, (2)
где 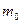 — масса покоя частицы.
— масса покоя частицы.
В релятивистском случае
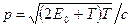 , (3)
, (3)
где 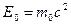 — энергия покоя частицы.
— энергия покоя частицы.
Формула (1) с учетом соотношений (2) и (3) запишется:
в нерелятивистском случае
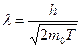 , (4)
, (4)
в релятивистском случае
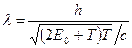 .
.
Сравним кинетические энергии электрона, прошедшего заданные в условии задачи разности потенциалов 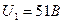 и
и 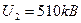 , с энергией покоя электрона и в зависимости от этого решим, какую из формул (4) или (5) следует применить для вычисления длины волны де Бройля.
, с энергией покоя электрона и в зависимости от этого решим, какую из формул (4) или (5) следует применить для вычисления длины волны де Бройля.
Как известно, кинетическая энергия электрона, прошедшего ускоряющую разность потенциалов U, 
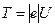 .
.
В первом случае 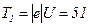 эВ=
эВ= 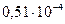 МэВ, что много меньше энергии покоя электрона
МэВ, что много меньше энергии покоя электрона 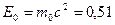 МэВ. Следовательно, в этом случае можно применить формулу (4). Для упрощения расчетов заметим, что
МэВ. Следовательно, в этом случае можно применить формулу (4). Для упрощения расчетов заметим, что 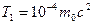 . Подставив это выражение в формулу (4), перепишем ее в виде
. Подставив это выражение в формулу (4), перепишем ее в виде
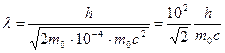 .
.
Учитывая, что 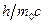 есть комптоновская длина волны
есть комптоновская длина волны 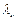 , получаем
, получаем
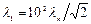 .
.
Так как 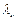 = 2,43 пм , то
= 2,43 пм , то
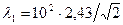 пм =171пм.
пм =171пм.
Во втором случае кинетическая энергия
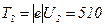 кэВ = 0,51 МэВ,
кэВ = 0,51 МэВ,
т.е. равна энергии покоя электрона. В этом случае необходимо применить релятивистскую формулу (5). Учитывая, что 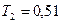 МэВ= =
МэВ= = 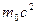 , по формуле (5) находим
, по формуле (5) находим
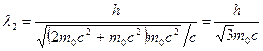 ,
,
или
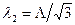 .
.
Подставим значение 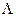 и произведем вычисления:
и произведем вычисления:
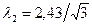 пм =1,40 пм.
пм =1,40 пм.
Пример 3. Электронный пучок ускоряется в электроннолучевой трубке разностью потенциалов 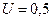 кВ. Принимая, что неопределенность импульса равна 0,1% от его числового значения, определить неопределенность координаты электрона. Являются ли в данных условиях электроны квантовой или классической частицей?
кВ. Принимая, что неопределенность импульса равна 0,1% от его числового значения, определить неопределенность координаты электрона. Являются ли в данных условиях электроны квантовой или классической частицей?
Ρ е ш е н и е. Согласно соотношению неопределенностей,
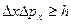 , (1)
, (1)
где 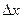 — неопределенность координаты электрона;
— неопределенность координаты электрона; 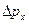 — неопределенность его импульса;
— неопределенность его импульса; 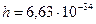 Дж
Дж 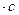 -постоянная Планка.
-постоянная Планка.
Кинетическая энергия электрона, прошедшего ускоряющую разность потенциалов 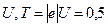 кэВ, т. е. электрон при данных условиях является нерелятивистской частицей (см. пример 3), и импульс электрона
кэВ, т. е. электрон при данных условиях является нерелятивистской частицей (см. пример 3), и импульс электрона
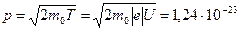 кг м/с.
кг м/с.
Согласно условию задачи, неопределенность импульса 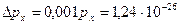 кг м/с, т.е.
кг м/с, т.е. 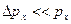 , и электрон при данных условиях является классической частицей. Из выражения (1) следует, что искомая неопределенность координаты электрона
, и электрон при данных условиях является классической частицей. Из выражения (1) следует, что искомая неопределенность координаты электрона
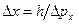 .
.
Вычисляя, получаем 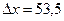 нм.
нм.
Пример 4. Волновая функция 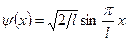 описывает основное состояние частицы в бесконечно глубоком прямоугольном ящике шириной
описывает основное состояние частицы в бесконечно глубоком прямоугольном ящике шириной 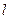 . Вычислить вероятность нахождения частицы в малом интервале
. Вычислить вероятность нахождения частицы в малом интервале 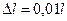 в двух случаях: 1 (вблизи стенки)
в двух случаях: 1 (вблизи стенки) 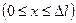 ; 2) в средней части ящика
; 2) в средней части ящика
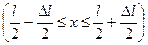
Решение. Вероятность того, что частица будет обнаружена в интервале dx (от х до х+dx), пропорциональна этому интервалу и квадрату модуля волновой функции, описывающей данное состояние, равна
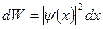 .
.
В первом случае искомая вероятность найдется интегрированием в пределах от 0 до 0,01 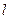 (рис. 4):
(рис. 4):
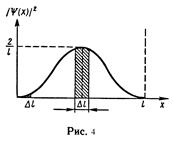
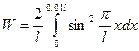 .
.
Знак модуля опущен, так как ψ — функция в данном случае не является комплексной.
Так как 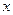 изменяется в интервале
изменяется в интервале 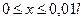 и, следовательно,
и, следовательно, 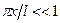 , справедливо приближенное равенство
, справедливо приближенное равенство
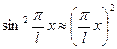 .
.
С учетом этого выражения (1) примет вид
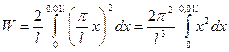 .
.
После интегрирования получим
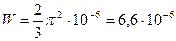 .
.
Во втором случае можно обойтись без интегрирования, так как квадрат модуля волновой функции вблизи ее максимума в заданном малом интервале 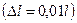 практически не изменяется. Искомая вероятность во втором случае определяется выражением
практически не изменяется. Искомая вероятность во втором случае определяется выражением
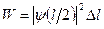 ,
,
или
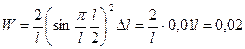 .
.
Пример 5. Нормированная волновая функция, описывающая 1s-состояние электрона в атоме водорода, имеет вид 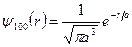 , где
, где 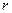 — расстояние электрона от ядра;
— расстояние электрона от ядра;
а - первый боровский радиус. Определить вероятность W обнаружения электрона в атоме внутри сферы радиусом 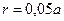
Решение. 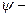 функция, описывающая 1s-состояние электрона в атоме водорода, сферически-симметрична (зависит только от
функция, описывающая 1s-состояние электрона в атоме водорода, сферически-симметрична (зависит только от 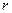 ). Поэтому элемент объема, отвечающий одинаковой плотности вероятности, выбирают в виде объема сферического слоя радиусам
). Поэтому элемент объема, отвечающий одинаковой плотности вероятности, выбирают в виде объема сферического слоя радиусам 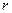 и толщиной
и толщиной 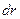 :
: 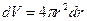 .
.
Вероятность обнаружить электрон в элементе объема 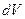
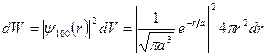 .
.
Вероятность W найдем, интегрируя dW в пределах от 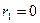 до
до 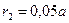 :
:
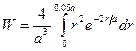 . (1)
. (1)
По условию задачи, 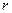 мало (
мало ( 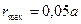 ;
; 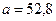 пм), поэтому сомножитель
пм), поэтому сомножитель 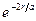 можно разложить в ряд
можно разложить в ряд
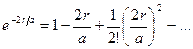 (2)
(2)
Подставив (2) в (1) и пренебрегая в (2) членами второго порядка, получим
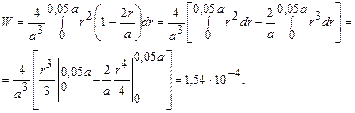 .
.
Таким образом, 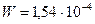 .
.
АТОМНОЕ ЯДРО. РАДИОАКТИВНОСТЬ. ЭЛЕМЕНТЫ ФИЗИКИ ТВЕРДОГО ТЕЛА
Массовое число ядра (число нуклонов в ядре)
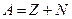 ,
,
где Ζ — зарядовое число (число протонов); N — число нейтронов.
Закон радиоактивного распада
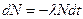 , или
, или 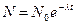 ,
,
где 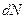 — число ядер, распадающихся за интервал времени
— число ядер, распадающихся за интервал времени 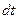 ; N — число ядер, не распавшихся к моменту времени
; N — число ядер, не распавшихся к моменту времени 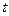 ;
; 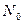 — число ядер в начальный момент (
— число ядер в начальный момент ( 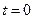 ); λ — постоянная радиоактивного распада.
); λ — постоянная радиоактивного распада.
Число ядер, распавшихся за время 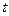 ,
,
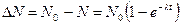 .
.
В случае, если интервал времени 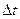 , за который определяется число распавшихся ядер; много меньше периода полураспада
, за который определяется число распавшихся ядер; много меньше периода полураспада 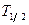 , то число распавшихся ядер можно определить по формуле
, то число распавшихся ядер можно определить по формуле
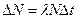 .
.
Зависимость периода полураспада от постоянной радиоактивного распада
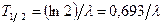 .
.
Среднее время τ жизни радиоактивного ядра, т. е. интервал времени, за который число нераспавшихся ядер уменьшается в е раз,
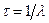 .
.
Число N атомов, содержащихся в радиоактивном изотопе,
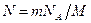 ,
,
где  — масса изотопа; Μ — молярная масса;
— масса изотопа; Μ — молярная масса; 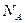 — постоянная Авогадро.
— постоянная Авогадро.
Активность А радиоактивного изотопа
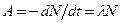 , или
, или 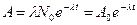 ,
,
где 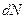 — число ядер, распадающихся за интервал времени
— число ядер, распадающихся за интервал времени 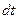 ;
; 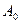 — активность изотопа в начальный момент времени.
— активность изотопа в начальный момент времени.
Удельная активность изотопа
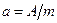 .
.
Дефект массы ядра
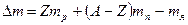 ,
,
где Ζ — зарядовое число (число протонов в ядре; А — массовое число (число нуклонов в ядре); (Α-Ζ) — число нейтронов в ядре; 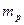 — масса протона;
— масса протона; 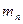 — масса нейтрона;
— масса нейтрона; 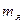 — масса ядра.
— масса ядра.
Энергия связи ядра
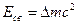 ,
,
где 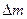 — дефект массы ядра;
— дефект массы ядра; 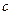 - скорость света в вакууме.
- скорость света в вакууме.
Во внесистемных единицах энергия связи ядра равна 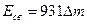 , где дефект массы
, где дефект массы 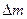 — в а. е. м.; 931 — коэффициент пропорциональности (1 а. е. м.
— в а. е. м.; 931 — коэффициент пропорциональности (1 а. е. м. 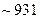 МэВ).
МэВ).
Концентрация электронов в зоне проводимости и дырок в валентной зоне
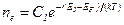 и
и 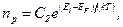
где Е2 – энергия, соответствующая дну зоны проводимости; Е1 – энергия, соответствующая верхней границе валентной зоны; ЕF – энергия Ферми; Т – термодинамическая температура; С1 и С2 – постоянные, зависящие от температуры и эффективных масс электронов проводимости и дырок (при равенстве последних С1 = С2).
Уровень Ферми в собственном полупроводнике
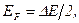
где 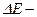 ширина запрещенной зоны.
ширина запрещенной зоны.
Удельная проводимость собственных полупроводников
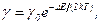
где 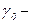 постоянная, характерная для данного полупроводника.
постоянная, характерная для данного полупроводника.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|