Примеры решения задач

Стр 1 из 6Следующая ⇒

ОПТИКА. КВАНТОВАЯ ПРИРОДА ИЗЛУЧЕНИЯ

Скорость света в среде

υ = c/n,

где c – скорость света в вакууме; n – показатель преломления среды.

Оптическая длина пути световой волны

L = nl,

где l – геометрическая длина пути световой волны в среде с показателем преломления n.

Оптическая разность хода двух световых волн

Δ = L₁ – L₂.

Зависимость разности фаз от оптической разности хода световых волн

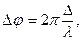
где λ – длина световой волны.

Условие максимального усиления света при интерференции

Δ = ±2kλ (k = 0, 1, 2, …).

Условие максимального ослабления света

Δ = ±(2k + 1) λ/2.

Оптическая разность хода световых волн, возникающая при отражении монохроматического света от тонкой пленки,

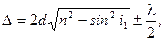
или

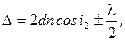
где d – толщина пленки; n – показатель преломления пленки; i₁ = угол падения; i₂ – угол преломления света в пленке.

Радиус светлых колец Ньютона в отраженном свете

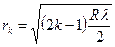(k = 1, 2, 3, …),

где k – номер кольца; R – радиус кривизны.

Радиус темных колец Ньютона в отраженном свете

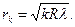
Угол φ отклонения лучей, соответствующих максимуму (световая полоса) при дифракции на одной щели, определяется из условия

asinφ = (2k + 1) λ/2 (k = 0, 1, 2, 3, …),

где a – ширина щели; k – порядковый номер максимума.

Угол φ отклонения лучей, соответствующий максимуму (светлая полоса) при дифракции света на дифракционной решетке, определяется из условия

dsinφ = ±k λ (k = 0, 1, 2, 3, …),

где d – период дифракционной решетки.

Разрешающая способность дифракционной решетки

R = λ /Δλ = kN,

где Δλ – наименьшая разность длин волн двух соседних спектральных линий (λ и λ +Δλ), при которой эти линии могут быть видны раздельно в спектре, полученном посредством данной решетки; N – полное число щелей решетки.

Формула Вульфа – Брэггов

2dsinθ = kλ,

где θ – угол скольжения (угол между направлением параллельного пучка рентгеновского излучения, падающего на кристалл, и атомной плоскостью в кристалле); d – расстояние между атомными плоскостями кристалла.

Закон Брюстера

tg ε_B = n₂₁,

где ε_B – угол падения, при котором отразившийся от диэлектрика луч полностью поляризован; n₂₁ – относительный показатель преломления второй среды относительно первой.

Закон Малюса

I = I₀cos² α,

где I₀ – интенсивность плоскополяризованного света, падающего на анализатор; I – интенсивность этого света после анализатора; α – угол между направлением колебаний электрического вектора света, падающего на анализатор, и плоскостью пропускания анализатора (если колебания электрического вектора падающего света совпадают с этой плоскостью, то анализатор пропускает данный свет без ослабления).

Угол поворота плоскости поляризации монохроматического света при прохождении через оптически активное вещество:

а) φ = αd (в твердых телах),

где α – постоянная вращения; d – длина пути, пройденного светом в оптически активном веществе;

б) φ = [α]ρd (в растворах),

где [α] – удельное вращение; ρ – массовая концентрация оптически активного вещества в растворе.

Закон Стефана – Больцмана

R_e = σT⁴,

где R_e – энергетическая светимость (излучательность) абсолютно черного тела; σ – постоянная Стефана – Больцмана; Т – термодинамическая температура.

Закон смещения Вина

λ _m = b/T,

где λ_m – длина волны, на которую приходится максимум энергии излучения; b – постоянная Вина.

Энергия фотона

ε = hν, или ε = ħω,

где h – постоянная Планка; ħ – постоянная Планка, деленная на 2π; ν – частота фотона; ω - циклическая частота.

Масса фотона

m = ε/c² = h/(cλ),

где с – скорость света в вакууме; λ – длина волны фотона.

Импульс фотона

p = mc = h/λ .

Формула Эйнштейна для фотоэффекта

hν = A + T_max = A+mv_max²/2,

где hν – энергия фотона, падающая на поверхность металла; А – работа выхода электрона; T_max – максимальная кинетическая энергия фотоэлектрона.

Красная граница фотоэффекта

ν₀ = А/h, или λ₀ = hc/A,

где ν₀ – минимальная частота света, при которой еще возможен фотоэффект; λ₀ – максимальная длина волны света, при которой еще возможен фотоэффект; h – постоянная Планка; с – скорость света в вакууме.

Формула Комптона

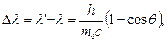
или

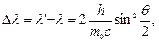
где λ – длина волны фотона, встретившегося со свободным или слабосвязанным электроном; λ` – длина волны фотона, рассеянного на угол θ после столкновения с электроном; m₀ – масса покоящегося электрона.

Комптоновская длина волны

Λ = h/(m₀c) (Λ = 2,436 пм).

Давление света при нормальном падении на поверхность

p = E_e(1 + ρ)/c = ω(1 + ρ),

где E_e – энергетическая освещенность (облученность); ω – объемная плотность энергии излучения; ρ – коэффициент отражения.

Примеры решения задач

Пример 1.На стеклянный клин с малым углом нормально к его грани падает параллельный пучок лучей монохроматического света с длиной волны λ = 0,6 мкм. Число m возникающих при этом интерференционных полос, приходящихся на отрезок клина длиной l, равно 10. Определить угол α клина.

Р е ш е н и е. Параллельный пучок света, падая нормально к грани клина, отражается как от верхней, так и от нижней грани. Эти отраженные пучки света когерентны. Поэтому на поверхности клина будут наблюдаться интерференционные полосы. Так как угол клина мал, то отраженные пучки 1 и 2 (рис. 1) будут практически параллельны.

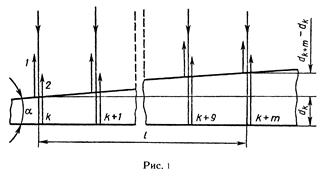
Темные полосы видны на тех участках клина, для которых разность хода лучей кратна нечетному числу половин длин волн:

Δ = (2k + 1)λ/2 (k = 0, ±1, ±2, …) (1)

Разность хода Δ двух волн складывается из разности оптических длин путей этих волн (2dncosε`₂) и половины длины волны (λ/2). Величина λ/2 представляет собой добавочную разность хода, возникающую при отражении световой волны 1 от оптически более плотной среды. Подставляя в формулу (1) разность хода Δ световых волн, получаем

2d_kn cos ε`₂+ λ/2 = (2k + 1) λ/2, (2)

где n – показатель преломления стекла (n = 1,5); d_k – толщина клина в том месте, где наблюдается темная полоса, соответствующая номеру k; ε`₂ – угол преломления.

Согласно условию, угол падения равен нулю; следовательно, и угол преломления ε`₂ равен нулю, а cos ε`₂ = 1. Раскрыв скобки в правой части равенства (2), после упрощения получим

2d_kn = kλ . (3)

Пусть произвольной темной полосе k-го номера соответствует толщина d_k клина, а темной полосе k + m-го номера – толщина d_k₊_m-го номера – толщина d_k₊_m клина. Тогда (см. рис. 1), учитывая, что m полос укладывается на расстоянии l, найдем

sin α = (d_{k + m} - d_k)/l . (4)

Выразим из (3) d_k и d_k₊_m и подставим их в формулу (4). Затем, учитывая, что sin α = α (из-за малости угла α), получим

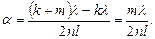
Подставляя значения физических величин, найдем

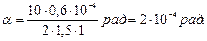
Выразим α в секундах. Для этого можно воспользоваться соотношением между радианом и секундой: 1 рад = 206 265`` ≈

≈ 2,06 · 10⁵``. Тогда

α = 2 · 10^-4 · 2,06 · 10⁵`` = 41,2``.

Пример 2.На дифракционную решетку в направлении нормали к ее поверхности падает монохроматический свет. Период решетки d = 2 мкм. Определить наибольший порядок дифракционного максимума, который дает эта решетка в случае красного (λ₁ = 0,7 мкм) и в случае фиолетового (λ₂ = 0,41 мкм) света.

Р е ш е н и е. Из формулы, определяющей положение главных максимумов дифракционной решетки, найдем порядок m дифракционного максимума:

m = (d sin φ)/λ , (1)

где d – период решетки; φ – угол дифракции; λ – длина волны монохроматического света. Так sin φ не может быть больше 1, то число m не может быть больше d/ λ, т. е.

m≤ d/ λ . (2)

Подставив в формулу (2) значения величин, получим:

m≤2/0,7 = 2,86 (для красных лучей);

m≤2/0,41 = 4,88 (для фиолетовых лучей).

Если учесть, что порядок максимумов является целым числом, то для красного света m_max = 2 и для фиолетового m_max = 4.

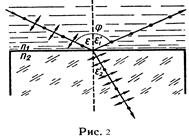Пример 3.Пучок естественного света падает на полированную поверхность стеклянной пластины, погруженной в жидкость. Отраженный от пластины пучок света образует угол φ = 97^о с падающим пучком (рис. 2).

Определить показатель преломления n₁ жидкости, если отраженный свет максимально поляризован.

Р е ш е н и е. 1. Согласно закону Брюстера, пучок света, отраженный от диэлектрика, максимально поляризован в том случае, если тангенс угла падения численно равен относительному показателю преломления tg ε = n₂₁, где n₂₁ – показатель преломления второй среды (стекла) относительно первой (жидкости).

Относительный показатель преломления равен отношению абсолютных показателей преломления. Следовательно, tg ε = n₂/n₁.

Так как угол падения равен углу отражения, то ε = φ/2 и, следовательно, tg (φ/2) = n₂/n₁, откуда

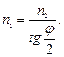
Произведем вычисления:

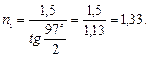
Пример 4.Два николя N₁ и N₂ расположены так, что угол между их плоскостями пропускания составляет α = 60^о. Определить, во сколько раз уменьшится интенсивность I_о естественного света: 1) при прохождении через один николь N₁; 2) при прохождении через оба николя. Коэффициент поглощения света в николе k = 0,05. Потери на отражении света не учитывать.

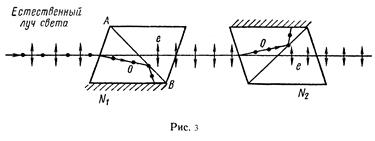
Р е ш е н и е. Естественный свет, падая на грань призмы Николя (рис. 3), расщепляется вследствие двойного лучепреломления на два пучка: обыкновенный и необыкновенный. Оба пучка одинаковы по интенсивности и полностью поляризованы. Плоскость колебаний необыкновенного пучка лежит в плоскости чертежа (плоскость главного сечения). Плоскость колебаний обыкновенного пучка перпендикулярна плоскости чертежа. Обыкновенный пучок света (о) вследствие полного отражения от границы АВ отбрасывается на зачерненную поверхность призмы и поглощается ею. Необыкновенный пучок (е) проходит через призму, уменьшая свою интенсивность вследствие поглощения. Таким образом, интенсивность света, прошедшего через призму,

I₁ = ½I₀(1 - k).

Относительное уменьшение интенсивности света получим, разделив интенсивность I₀ естественного света, падающего на первый николь, на интенсивность I₁ поляризованного света:

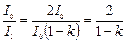. (1)

Произведем вычисления:

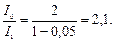
Таким образом, интенсивность уменьшается в 2,1 раза.

2. Плоскополяризованный пучок света интенсивности I₁ падает на второй николь N₂ и также расщепляется на два пучка различной интенсивности: обыкновенной и необыкновенной. Обыкновенный пучок полностью поглощается призмой, поэтому интенсивность его нас не интересует. Интенсивность I₂ необыкновенного пучка, вышедшего из призмы N₂, определяется законом Малюса (без учета поглощения света во втором николе):

I₂ = I₁ cos²α,

где α – угол между плоскостью колебаний в поляризованном пучке и плоскостью пропускания николя N₂.

Учитывая потери интенсивности на поглощение во втором николе, получаем

I₂ = I₁(1 - k)cos² α .

Искомое уменьшение интенсивности при прохождение света через оба николя найдем, разделив интенсивность I₀ естественного света на интенсивность I₂ света, прошедшего систему из двух николей:

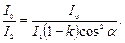
Заменяя отношение I₀/I₁ его выражением по формуле (1), получаем

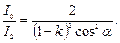
Произведем вычисления:

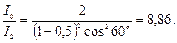
Таким образом, после прохождения света через два николя интенсивность его уменьшится в 8,86 раза.

Пример 5.Длина волны, на которую приходится максимум энергии в спектре излучения черного тела, λ₀ = 0,58 мкм. Определить энергетическую светимость (излучаемость) R_e поверхности тела.

Р е ш е н и е. Энергетическая светимость R_e абсолютно черного тела в соответствии с законом Стефана-Больцмана пропорциональна четвертой степени термодинамической температуры и выражается формулой

R_e = σТ⁴, (1)

где σ – постоянная Стефана-Больцмана; Т – термодинамическая температура.

Температуру Т можно вычислить с помощью закона смещения Вина:

λ₀ = b/Т, (2)

где b – постоянная закона смещения Вина.

Используя формулы (2) и (1), получаем

R_e = σ(b/λ₀)⁴. (3)

Произведем вычисления:

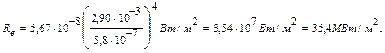
Пример 6.Определить максимальную скорость υ_max фотоэлектронов, вырываемых с поверхности серебра: 1) ультрафиолетовым излучением с длиной волны λ₁ = 0,155 мкм; 2) γ-излучением с длиной волны λ₂ = 1 пм.

Р е ш е н и е. Максимальную скорость фотоэлектронов можно определить из уравнения Эйнштейна для фотоэффекта:

ε = А + Т_max, (1)

где ε – энергия фотонов, падающих на поверхность металла; А – работа выхода; Т_max – максимальная кинетическая энергия фотоэлектронов.

Энергия фотона вычисляется также по формуле

ε = hc/λ , (2)

где h – постоянная Планка; с – скорость света в вакууме; λ – длина волны.

Кинетическая энергия электрона может быть выражена или по классической формуле

T = m₀υ²/2, (3)

или по релятивистской формуле

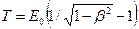
, (4)

в зависимости от того, какая скорость сообщается фотоэлектрону. Скорость фотоэлектрона зависит от энергии фотона, вызывающего фотоэффект: если энергия ε фотона много меньше энергии покоя Е₀ электрона, то может быть применен формула (3), если же ε сравнима по величине с Е₀, то вычисление по формуле (3) приводит к ошибке, поэтому нужно пользоваться формулой (4).

1. Вычисление энергии фотона ультрафиолетового излучения по формуле (2):

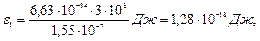
или

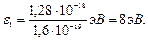
Полученная энергия фотона (8 эВ) много меньше энергии покоя электрона (0,51 МэВ). Следовательно, для данного случая кинетическая энергия фотоэлектрона в формуле (1) может быть выражена по классической формуле (3):

ε₁ = А + m₀υ²_max/2,

откуда

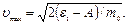
Проверим, дает ли полученная формула единицу скорости. Для этого в правую часть формулы (5) вместо символов величин подставим обозначения единиц:

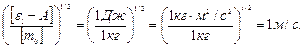
Найденная единица является единицей скорости.

Подставляя значения величин в формулу (5), найдем

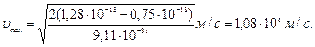
2. Вычислим энергию γ-излучения:

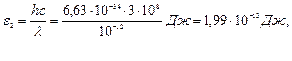
или во внесистемных единицах

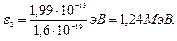
Работа выхода электрона (А = 4,7 эВ) пренебрежимо мала по сравнению с энергией фотона (ε₂ = 1,24 МэВ), поэтому можно принять, что максимальная кинетическая энергия электрона равна энергии фотона: T_max = ε₂ = 1,24 МэВ. Так как в данном случае кинетическая энергия электрона больше его энергии покоя, то для вычисления скорости электрона следует взять релятивистскую формулу кинетической энергии (4). Из этой формулы найдем

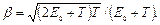
Заметив, что υ = cβ и T_max = ε₂, получим

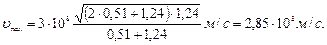
Пример 7.В результате эффекта Комптона фотон при соударении с электроном был рассеян на угол θ = 90^о. Энергия рассеянного фотона ε₂ = 0,4 МэВ. Определить энергию фотона ε₁ до рассеяния.

Р е ш е н и е. Для определения энергии первичного фотона восполь зуемся формулой Комптона:

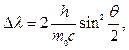
(1)
где Δλ = λ₂ – λ₁ – изменение длины волны фотона в результате рассеяния на свободном электроне; h – постоянная Планка; m₀ – масса покоя электрона; с – скорость света в вакууме; θ – угол рассеяния фотона.

Преобразуем формулу (1): 1) заменим в ней Δλ на λ₂ – λ₁; 2) выразим длины волны λ₁ и λ₂ через энергии ε₁ и ε₂ соответствующих фотонов, воспользовавшись формулой ε = hc/λ; 3) умножим числитель и знаменатель правой части формулы на с. Тогда

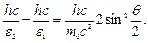
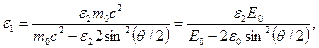Сократим на hc и выразим из этой формулы искомую энергию:

(2)

где Е₀ = m₀c² – энергия покоя электрона.

Вычисления по формуле (2) удобнее вести во внесистемных единицах. Так как для электрона Е₀ = 0,511 МэВ, то

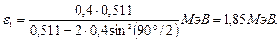
Пример 8.Пучок монохроматического света с длиной волны λ = 663 нм падает нормально на зеркальную плоскую поверхность. Поток Ф_е = 0,6 Вт. Определить: 1) силу давления F, испытываемую этой поверхностью; 2) число фотонов, ежесекундно падающих на поверхность.

Р е ш е н и е. 1. Сила светового давления на поверхность равна произведению светового давления p на площадь S поверхности:

F = pS. (1)

Световое давление может быть найдено по формуле

p = E_e(ρ + 1)/c, (2)

где E_e – энергетическая освещенность; с – скорость света в вакууме; ρ – коэффициент отражения.

Подставляя правую часть выражения (2) в формулу (1), получаем

F = E_eS(ρ + 1)/c. (3)

Так как E_eS представляет собой поток излучения Ф_е, то

F = Ф_е(ρ + 1)/c. (4)

Произведем вычисления, учитывая, что для зеркальной поверхности ρ = 1:

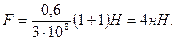
2. Произведение энергии ε одного фотона на число фотонов n₁, ежесекундно падающих на поверхность, равно мощности излучения, т. е. поток излучения: Ф_е = εn₁, а так как энергия фотона ε = hc/λ, то

Ф_е = hcn₁/λ,

откуда

n₁ = Ф_еλ/(hc). (5)

Произведем вычисления:

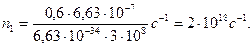
ЭЛЕМЕНТЫ АТОМНОЙ ФИЗИКИ И КВАНТОВОЙ МЕХАНИКИ.

12 3 4 5 6 Следующая ⇒