Хелпикс

Главная

Контакты

Случайная статья



ФИЗИКА ТВЕРДОГО ТЕЛА

⇐ ПредыдущаяСтр 2 из 6Следующая ⇒


ФИЗИКА ТВЕРДОГО ТЕЛА

 

Боровская теория водородоподобного атома. Момент импульса электрона (второй постулат Бора)

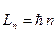, или ,

где m— масса электрона;  — скорость электрона на n-й орбите; 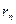 — радиус n-й стационарной орбиты; 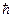— постоянная Планка; n — глав­ное квантовое число (n=1,2,3,…).

Радиус n-й стационарной орбиты

,

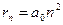где  — первый боровский радиус.

  Энергия электрона в атоме водорода

,

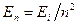где  — энергия ионизации атома водорода.

Энергия, излучаемая или поглощаемая атомом водорода,

,

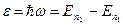или

,

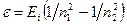где 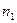 и 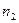 — квантовые числа, соответствующие энерге­тическим уровням, между которыми совершается переход электрона в атоме.

  Спектроскопическое волновое число

,

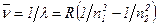где λ — длина волны излучения или поглощения атомом; R— постоян­ная Ридберга.

Волновые свойства частиц. Длина волны де Бройля

,

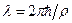где ρ — импульс частицы.

Импульс частицы и его связь с кинетической энер­гией Т:

а) ; ;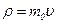

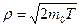б) ; ,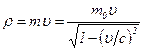

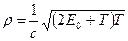где 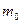 — масса покоя частицы; m — релятивистская мас­са; υ - ско­рость частицы; с — скорость света в вакууме;  — энергия покоя частицы .

 Соотношение неопределенностей:

а) 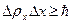 (для координаты и импульса),

где 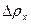 — неопределенность проекции импульса на ось Х;  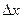— неопределенность координаты;

б) 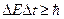 (для энергии и времени),

Одномерное уравнение Шредингера для стационарных состояний

,

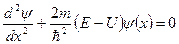где 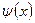- волновая функция, описывающая состояние частицы; -масса частицы; E-полная энергия; - потенциальная энергия частицы.

Плотность вероятности

,

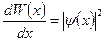где 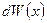 — вероятность того, что частица может быть обнаружена вблизи точки с координатой  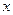на участке .

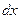Вероятность обнаружения частицы в интервале от х1 до х2

.

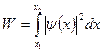Решение уравнения Шредингера для одномерного,  бесконечно глубокого, прямоугольного потенциального ящика:             

а) 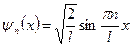                     (собственная нормированная вол­новая функция);

б) 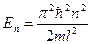                                 (собственное значение энергии);

где n — квантовое число (n=1, 2, 3, ...); 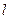 — ширина ящика. В области x < 0 и x > l,  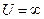и .

 


⇐ Предыдущая123456Следующая ⇒
  

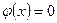© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.