
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Парабола. Уравнения кривых второго порядка с осями симметрии, параллельными осям координат. Приведение общего уравнения кривой второго порядка, не содержащего члена с произведением текущих координат, . к каноническому виду
4 Парабола
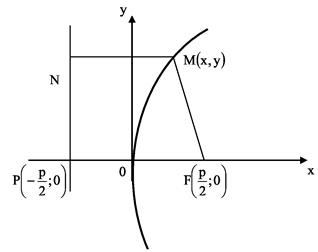
Параболой называется множество всех точек на плоскости, каждая из которых одинаково удалена от заданной точки этой же плоскости, называемой фокусом, и от заданной прямой, называемой директрисой.
Число p>0 называется параметром параболы и равно расстоянию от фокуса F до директрисы l.
Если фокус параболы находится в точке 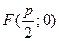 , а директриса N имеет уравнение
, а директриса N имеет уравнение 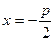 , то такая парабола имеет каноническое уравнение:
, то такая парабола имеет каноническое уравнение:
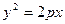 , (18)
, (18)
Точка 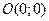 называется вершиной параболы.
называется вершиной параболы.
Ось 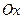 - ось симметрии параболы.
- ось симметрии параболы.
Расстояние от точки 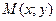 параболы до фокуса F (фокальный радиус) вычисляется по формуле
параболы до фокуса F (фокальный радиус) вычисляется по формуле
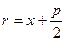 . (19)
. (19)
|
Парабола, симметричная относительно оси 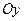 , с вершиной в начале координат, имеет уравнение
, с вершиной в начале координат, имеет уравнение
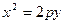 , (20)
, (20)
Фокус параболы находится в точке 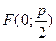 .
.
Уравнение директрисы этой параболы
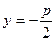 . (21)
. (21)
Фокальный радиус точки 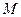 параболы
параболы
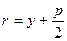 . (22)
. (22)
Графики парабол 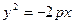 и
и 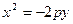 строятся в полуплоскостях, соответствующих отрицательным значениям переменных
строятся в полуплоскостях, соответствующих отрицательным значениям переменных 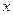 и
и 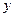 .
.
Пример 4.1.
Найти уравнение параболы, симметричной относительно оси 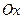 ,фокус которой находится в точке пересечения прямой
,фокус которой находится в точке пересечения прямой 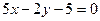 с осью
с осью 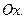
Решение.
Найдем точку пересечения прямой 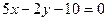 с осью
с осью 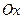 .
.
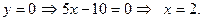
Т.к. расстояние от фокуса параболы до начала координат равно 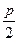 , то
, то 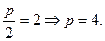
Используя формулу (18), запишем уравнение параболы: 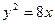 .
.
Задачи для самостоятельного решения:
1. Определить величину параметра и расположение относительно координатных осей следующих парабол: 1) 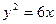 ; 2)
; 2) 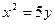 ; 3)
; 3) 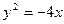 ; 4)
; 4) 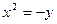 .
.
2. Составить уравнение параболы, если дан фокус 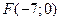 и уравнение директрисы
и уравнение директрисы 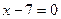 .
.
3. На параболе 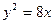 найти точку, расстояние которой от директрисы параболы равно 4.
найти точку, расстояние которой от директрисы параболы равно 4.
4. Составить уравнение параболы с вершиной в начале координат, симметричной относительно оси 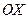 и отсекающей на прямой
и отсекающей на прямой 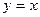 хорду длиной
хорду длиной 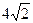 .
.
5. На параболе 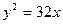 найти точку, расстояние которой от прямой
найти точку, расстояние которой от прямой 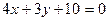 равно 2.
равно 2.
6. Установить, какие линии определяются следующими уравнениями:
1) 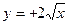 ; 2)
; 2) 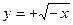 ; 3)
; 3) 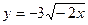 ; 4)
; 4) 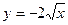 ; 5)
; 5) 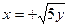 ;
;
6) 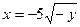 ; 7)
; 7) 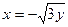 ; 8)
; 8) 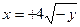 . Изобразить эти линии на чертеже.
. Изобразить эти линии на чертеже.
5 Уравнения кривых второго порядка с осями симметрии, параллельными осям координат. Приведение общего уравнения кривой второго порядка, не содержащего члена с произведением текущих координат,
к каноническому виду
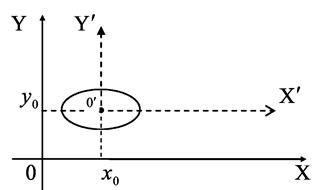
Даны две прямоугольные системы координат 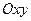 и
и 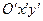 со свойствами: оси
со свойствами: оси 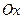 и
и 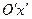 , а также
, а также 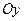 и
и 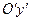 параллельны и одинаково направлены, а начало
параллельны и одинаково направлены, а начало 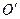 системы
системы 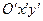 имеет известные координаты
имеет известные координаты 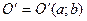 относительно системы
относительно системы 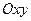 .
.
Тогда координаты 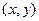 и
и 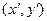 произвольной точки
произвольной точки 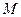 плоскости связаны соотношениями:
плоскости связаны соотношениями:
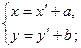
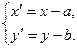 (23)
(23)
Формулы (18) называются формулами преобразования координат при параллельном переносе осей координат.
Уравнение эллипса с полуосями 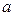 и
и 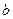 , центром в точке
, центром в точке 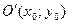 и осями симметрии, параллельными координатным осям, имеет вид:
и осями симметрии, параллельными координатным осям, имеет вид:
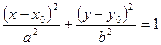 , (24)
, (24)
|
Уравнение гиперболы с осями, параллельными координатным, имеет вид:
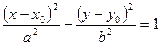 , (25)
, (25)
где 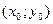 - координаты центра гиперболы.
- координаты центра гиперболы.
Уравнение параболы с осью симметрии, параллельной оси абсцисс, имеет вид:
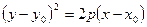 , (26)
, (26)
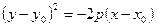 , (27)
, (27)
Если ось параболы параллельна оси ординат, то
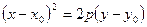 , (28)
, (28)
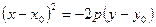 , (29)
, (29)
Пример 5.1.
Уравнение линии 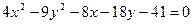 привести к каноническому виду и построить ее.
привести к каноническому виду и построить ее.
Решение.
Выделим в правой части уравнения полные квадраты:
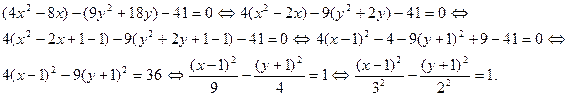
Уравнение определяет гиперболу с центром в точке 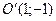 , действительной полуосью
, действительной полуосью 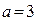 и мнимой полуосью
и мнимой полуосью 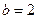 . Прямые
. Прямые 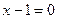 и
и 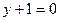 являются осями симметрии гиперболы, параллельными координатным осям
являются осями симметрии гиперболы, параллельными координатным осям 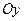 и
и 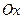 соответственно.
соответственно.
Построим основной прямоугольник гиперболы со сторонами 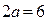 и
и 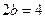 с центром в точке
с центром в точке 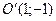 (рис. 8). Диагонали этого прямоугольника являются асимптотами гиперболы.
(рис. 8). Диагонали этого прямоугольника являются асимптотами гиперболы.
|
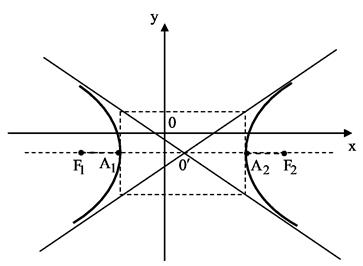
Найдем уравнения асимптот. Так как асимптоты проходят через точку 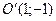 и имеют угловые коэффициенты
и имеют угловые коэффициенты 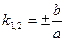 (см. уравнение (12)), то уравнения прямых запишутся следующим образом:
(см. уравнение (12)), то уравнения прямых запишутся следующим образом:
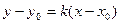 ;
; 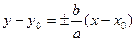 ;
; 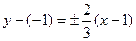 ;
; 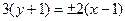 .
.
Получим уравнения асимптот: 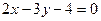 и
и 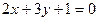 .
.
Найдем вершины гиперболы. В системе координат 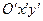 :
: 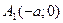 ,
, 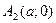 , т.е.
, т.е. 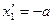 ,
, 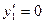 ;
; 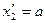 ,
, 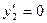 ;
; 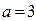 . Из формул (23) получим:
. Из формул (23) получим:
Точка 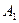 :
: 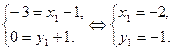 Точка
Точка 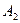 :
: 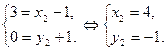
Итак, в системе координат 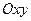 вершины гиперболы выглядят следующим образом:
вершины гиперболы выглядят следующим образом: 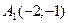 ,
, 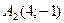 .
.
Найдем фокусы гиперболы. Из формулы (10) имеем: 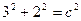 ;
; 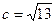 . Координаты фокусов в системе координат
. Координаты фокусов в системе координат 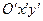 :
: 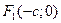 и
и 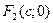 .
.
Точка 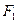 :
: 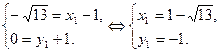 Точка
Точка 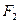 :
: 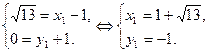
В системе координат 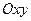 координаты фокусов:
координаты фокусов:  ,
, 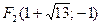
По формуле (11) вычислим эксцентриситет: 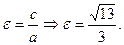
Задачи для самостоятельного решения:
Каждое из следующих уравнений путем параллельного переноса привести к каноническому виду; определить тип; изобразить на чертеже расположение геометрических образов относительно старых и новых координат. Определить основные характеристики.
1. 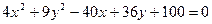 9.
9. 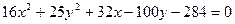
2. 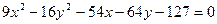 10.
10. 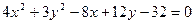
3. 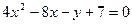 11.
11. 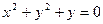
4. 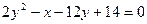 12.
12. 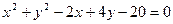
5. 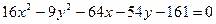 13.
13. 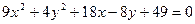
6. 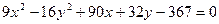 14.
14. 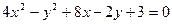
7. 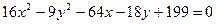 15.
15. 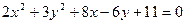
8. 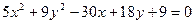 16.
16. 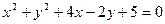
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
1. Письменный Д. Т.
Конспект лекций по высшей математике: полный курс / Д. Т. Письменный . - 9-е изд. - М.: Айрис-Пресс, 2008. – 280с.- Ч. 1.
2. Лунгу К.Н.
Сборник задач по высшей математике: учеб. пособие / К.Н.Лунгу и др.- 7-е изд..- М.: Айрис Пресс, 2008.- 574 с.
3. Лунгу К.Н.
Высшая математика. Руководство к решению задач: учеб. пособие / К.Н.Лунгу, Е.В.Макаров - 2-е изд.- М.: ФИЗМАТЛИТ, 2005.- 216 с.- Ч. 1.
4. Садовничий Ю.В.
Аналитическая геометрия. Курс лекций с задачами: учеб. издание / Ю.В. Садовничий, В.В.Федорчук - М.: Издательство «Экзамен», 2009. – 350 c.
5. Клетеник Д.В.
Сборник задач по аналитической геометрии: учеб. пособие / Д.В. Клетеник - 14-е изд..-М.: Наука.- 1986. - 224 с.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|