- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Эллипс. Гипербола
2 Эллипс
Эллипсом называется множество всех точек плоскости, сумма расстояний от каждой из которых до двух данных точек этой же плоскости, называемых фокусами, есть величина постоянная, большая, чем расстояние между фокусами.
Каноническое уравнение эллипса имеет вид:
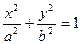 , (4)
, (4)
где  - большая полуось,
- большая полуось, 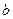 - малая полуось эллипса,
- малая полуось эллипса, 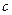 - фокусное расстояние. Из определения следует, что
- фокусное расстояние. Из определения следует, что 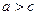 . Числа
. Числа  ,
, 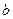 ,
, 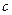 связаны соотношением
связаны соотношением
 . (5)
. (5)
Отсюда следует, что  .
.
Координаты фокусов 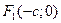 ,
, 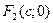 . Фокусы эллипса лежат на оси
. Фокусы эллипса лежат на оси 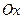 .
.
Точки A, B, C, D называются вершинами эллипса, точка O – центром эллипса.
Из уравнения (4) следует, что каждое слагаемое в левой части не превосходит единицы, т.е. имеют место неравенства 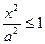 и
и 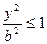 или
или 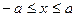 и
и 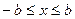 . Следовательно, все точки эллипса лежат внутри прямоугольника, образованного прямыми
. Следовательно, все точки эллипса лежат внутри прямоугольника, образованного прямыми 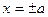 ,
, 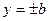 .
.
Если 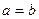 , то уравнение (4) определяет окружность
, то уравнение (4) определяет окружность 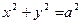 , рассматриваемую как частный случай эллипса.
, рассматриваемую как частный случай эллипса.
Важными характеристиками эллипса являются:
- эксцентриситет показывает степень вытянутости, обозначается буквой 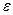 («эпсилон»):
(«эпсилон»):
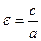 (0<
(0< 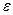 <1) (6)
<1) (6)
если 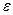 ~ 0, то эллипс почти круглый, т.е. близок к окружности,
~ 0, то эллипс почти круглый, т.е. близок к окружности,
если 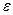 = 0, т.е.
= 0, т.е. 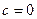 ,
, 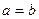 , то эллипс превращается в окружность,
, то эллипс превращается в окружность,
если 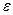 ~ 1, то эллипс сплющенный, близок к отрезку
~ 1, то эллипс сплющенный, близок к отрезку 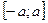 .
.
- директрисы эллипса – прямые с уравнениями
 ,
, 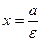 . (7)
. (7)
- фокальные радиусы – расстояния 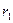 и
и 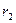 от произвольной точки
от произвольной точки 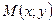 эллипса до его фокусов (
эллипса до его фокусов ( 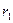 до левого,
до левого, 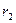 до правого) определяются формулами:
до правого) определяются формулами:
 ,
, 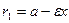
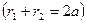 . (8)
. (8)
Если фокусы эллипса лежат на оси 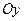 , то
, то 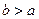 , большая ось
, большая ось 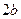 лежит на оси
лежит на оси 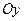 , малая ось
, малая ось 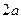 - на оси
- на оси 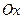 ,
, 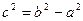 ,
, 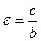 , уравнения директрис
, уравнения директрис 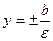 . Координаты фокусов
. Координаты фокусов 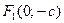 ,
,  .
.
 | |||
| |||
Пример 2.1.
Составить уравнение эллипса, симметричного относительно координатных осей, проходящего через точку  и имеющего эксцентриситет
и имеющего эксцентриситет 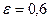 .
.
Решение.
Из формул (4)-(6) имеем систему уравнений относительно параметров а, b:
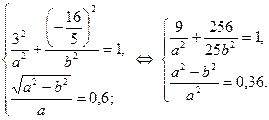
Из второго уравнения находим:
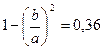 , т.е.
, т.е. 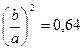 , т.е.
, т.е. 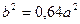 .
.
Подставляя это в первое уравнение, получим 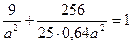 ,
, 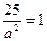 , тогда
, тогда 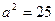 ,
, 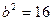 ,
, 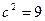 .
.
Уравнение эллипса 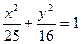 .
.
Пример 2.2.
Составить уравнение эллипса, симметричного относительно координатных осей и проходящего через точки 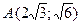 и
и  . Найти эксцентриситет эллипса, расстояния от точки
. Найти эксцентриситет эллипса, расстояния от точки  до фокусов и уравнения его директрис.
до фокусов и уравнения его директрис.
Решение.
Параметры a и b найдем, подставив в уравнение (4) координаты точек A и B. Это приводит к системе
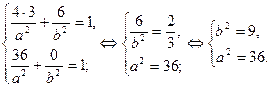
Отсюда, с учетом 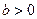 ,
, 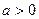 находим:
находим: 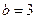 ,
, 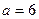 .
.
Каноническое уравнение эллипса найдено: 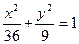 .
.
Фокусное расстояние 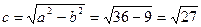 .
.
Эксцентриситет равен 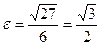 .
.
Расстояния от точки 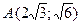 до фокусов:
до фокусов:
 ;
; 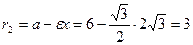 .
.
Уравнения директрис: 
левая директриса: 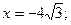 правая директриса:
правая директриса: 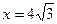 .
.
Задачи для самостоятельного решения:
1. Дан эллипс  . Найти: 1) его полуоси; 2) фокусы; 3) эксцентриситет; 4) уравнения директрис.
. Найти: 1) его полуоси; 2) фокусы; 3) эксцентриситет; 4) уравнения директрис.
2. Составить уравнение эллипса, проходящего через точку  , имеющего эксцентриситет
, имеющего эксцентриситет  .
.
3. На прямой 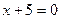 найти точку, одинаково удаленную от левого фокуса и верхней вершины эллипса
найти точку, одинаково удаленную от левого фокуса и верхней вершины эллипса 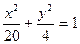 .
.
4. Составить уравнение геометрического места точек, расстояния которых от точки 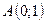 в два раза меньше расстояния до прямой
в два раза меньше расстояния до прямой 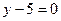 .
.
3 Гипербола
Гиперболой называется множество всех точек плоскости, модуль разности расстояний от каждой из которых до двух заданных точек этой же плоскости, называемых фокусами, есть величина постоянная, меньшая, чем расстояние между фокусами.
|
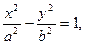 (9)
(9)
где 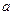 - действительная полуось,
- действительная полуось, 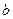 - мнимая полуось гиперболы,
- мнимая полуось гиперболы, 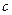 - фокусное расстояние. Числа
- фокусное расстояние. Числа 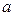 ,
, 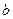 ,
, 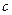 связаны соотношением
связаны соотношением
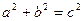 . (10)
. (10)
Координаты фокусов 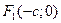 ,
, 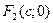 .
.
Точки 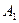 и
и 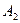 называются вершинами гиперболы, точка O – центром гиперболы.
называются вершинами гиперболы, точка O – центром гиперболы.
Важными характеристиками гиперболы являются:
- эксцентриситет
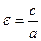 (1<
(1< 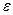 <
< 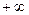 ) (11)
) (11)
если 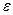 ~ 1, то ветви гиперболы широкие, почти вертикальные,
~ 1, то ветви гиперболы широкие, почти вертикальные,
если 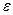 ~
~ 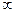 , то ветви гиперболы узкие, гипербола приближается к оси Ox.
, то ветви гиперболы узкие, гипербола приближается к оси Ox.
- асимптоты
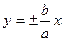 . (12)
. (12)
Прямоугольник 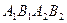 , центр которого совпадает с точкой О, а стороны равны и параллельны осям гиперболы называется основным прямоугольником гиперболы. Диагонали основного прямоугольника лежат на асимптотах.
, центр которого совпадает с точкой О, а стороны равны и параллельны осям гиперболы называется основным прямоугольником гиперболы. Диагонали основного прямоугольника лежат на асимптотах.
- директрисы гиперболы – прямые, параллельные мнимой оси гиперболы и отстоящие от нее на расстоянии, равном 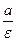 . Уравнения директрис:
. Уравнения директрис:
 ,
, 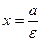 . (13)
. (13)
- фокальные радиусы определяются формулами:
для точек правой ветви гиперболы:
 ,
, 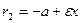 ; (14)
; (14)
для точек левой ветви:
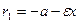 ,
, 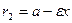 . (15)
. (15)

|
Если 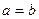 , то гипербола (9) называется равносторонней (равнобочной). Ее уравнение принимает вид
, то гипербола (9) называется равносторонней (равнобочной). Ее уравнение принимает вид
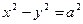 . (16)
. (16)
Если фокусы гиперболы лежат на оси 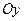 , то уравнение гиперболы имеет вид:
, то уравнение гиперболы имеет вид:
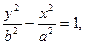 (17) эксцентриситет этой гиперболы равен
(17) эксцентриситет этой гиперболы равен 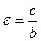 , асимптоты определяются уравнениями
, асимптоты определяются уравнениями 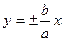 , уравнения директрис
, уравнения директрис 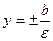 . Гипербола (17) называется сопряженной гиперболе (9).
. Гипербола (17) называется сопряженной гиперболе (9).
Пример 3.1.
Дано уравнение гиперболы 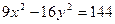 . Найти:
. Найти:
1) длины его полуосей;
2) координаты фокусов;
3) эксцентриситет гиперболы;
4) уравнения асимптот и директрис;
5) фокальные радиусы точки 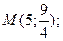
6) на гиперболе найти точку, для которой расстояние от левого фокуса в 3 раза больше, чем от правого.
Решение.
Разделив обе части уравнения 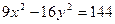 на
на 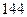 , приведем уравнение гиперболы к каноническому виду:
, приведем уравнение гиперболы к каноническому виду: 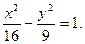 Отсюда:
Отсюда:
1) 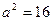 ,
, 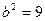 , т.е. действительная полуось
, т.е. действительная полуось  , мнимая полуось
, мнимая полуось 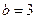 .
.
2) Используя соотношение (10), находим 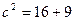 , т.е.
, т.е. 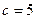 . Запишем фокусы гиперболы:
. Запишем фокусы гиперболы: 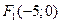 ,
, 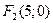 .
.
3) По формуле (11) находим эксцентриситет гиперболы 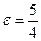 .
.
4) Уравнения асимптот и директрис найдем по формулам (12) и (13):  и
и 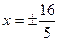 .
.
5) точка 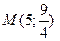 лежит на правой ветви гиперболы
лежит на правой ветви гиперболы 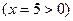 , используем формулы (14):
, используем формулы (14): 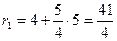 ,
, 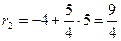 .
.
6) Найдем на гиперболе точку 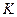 такую, что
такую, что  . Используя формулы (14) и
. Используя формулы (14) и  , получим:
, получим:
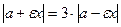 ;
;
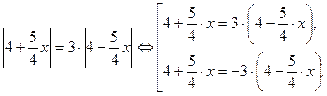
Находим 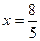 и
и 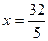 .
.
Поскольку 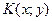 лежит на гиперболе
лежит на гиперболе 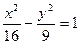 , то ординаты соответствующих точек найдем из этого уравнения при найденных значениях x:
, то ординаты соответствующих точек найдем из этого уравнения при найденных значениях x:
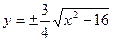 и, если
и, если 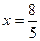 , то
, то 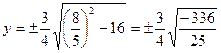 (это число не существует в нужном нам смысле), а если
(это число не существует в нужном нам смысле), а если 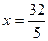 , то
, то 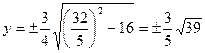 .
.
Итак, получили две точки на гиперболе, удовлетворяющие данным условиям: 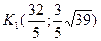 и
и 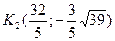 .
.
Пример 3.2.
Составить уравнение гиперболы, симметричной относительно координатных осей, которая проходит через точку 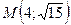 и ее асимптоты имеют уравнения
и ее асимптоты имеют уравнения 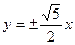 .
.
Решение.
Подставим координаты точки 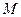 в уравнение (9):
в уравнение (9): 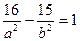 .
.
Уравнения асимптот гиперболы 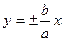 , поэтому
, поэтому  , тогда
, тогда 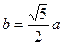 . Получим систему двух уравнений:
. Получим систему двух уравнений:

Запишем уравнение гиперболы: 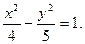
Задачи для самостоятельного решения:
1. Найти уравнение гиперболы, вершины и фокусы которой находятся в соответствующих фокусах и вершинах эллипса 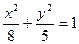 .
.
2. Определить эксцентриситет равносторонней гиперболы.
3. Составить уравнение гиперболы, если ее эксцентриситет равен 2 и фокусы совпадают с фокусами эллипса 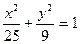 .
.
4. Дана гипербола 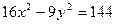 . Найти: 1) полуоси
. Найти: 1) полуоси 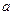 и
и 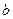 ; 2) фокусы;
; 2) фокусы;
3) эксцентриситет; 4) уравнения асимптот; 5) уравнения директрис.
5. Дана гипербола 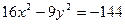 . Найти: 1) полуоси
. Найти: 1) полуоси 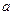 и
и 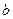 ; 2) фокусы;
; 2) фокусы;
3) эксцентриситет; 4) уравнения асимптот; 5) уравнения директрис.
6. Установить, какие линии определяются следующими уравнениями:
1) 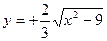 ; 2)
; 2)  ; 3)
; 3)  ; 4)
; 4)  .
.
Изобразить эти линии на чертеже.
7. Дана точка 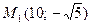 на гиперболе
на гиперболе 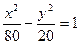 . Составить уравнения прямых, на которых лежат фокальные радиусы точки
. Составить уравнения прямых, на которых лежат фокальные радиусы точки 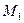 .
.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|