Хелпикс

Главная

Контакты

Случайная статья



Кривые второго порядка

Стр 1 из 4Следующая ⇒


 

Федеральное государственное бюджетное

образовательное учреждение

высшего профессионального образования

«Башкирский государственный аграрный университет»

 

Кафедра математики

 

Математика

МЕТОДИЧЕСКИЕ УКАЗАНИЯ по теме:

 

«Кривые второго порядка»

 

для всех направлений бакалавриата

 

 

 

Уфа-2012

 

 

ООУДК 51

ББК 22.1

М 33

 

Рекомендовано к изданию методической комиссией механического факультета (протокол № 9 от 27 июля 2012 года ) и заседанием кафедры математики (протокол № 7 от 10 апреля 2012 года)

 

Составитель: ассистент Галиуллина Э.В.

 

Рецензент: доцент кафедры физики Юмагужин Р.Ю.

 

Ответственный за выпуск: зав. кафедрой математики

                                           доцент Лукманов Р.Л.

 

1    Кривые второго порядка

Рассмотрим линии, определяемые уравнениями второй степени относительно текущих координат

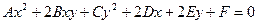                                                            (1)

Коэффициенты уравнения – действительные числа, но по крайней мере одно из чисел А, В или С отлично от нуля. Такие линии называются линиями (кривыми) второго порядка.

Общее уравнение второго порядка (1) определяет на плоскости (если не считать случаев вырождения и распадения) следующие кривые: окружность, эллипс, гиперболу, параболу.

Теорема 1.

Для любой линии второго порядка существует прямоугольная система координат, в которой уравнение этой линии имеет один из следующих видов:

1) 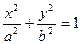, эллипс;

2) 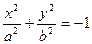, мнимый эллипс;

3) 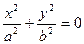, пара мнимых пересекающихся прямых;

4) 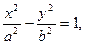  гипербола;

5) 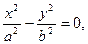  пара пересекающихся прямых;

6) 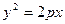, парабола;

7) 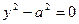, пара параллельных прямых;

8) 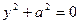, пара мнимых параллельных прямых;

9) 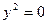, пара совпадающих прямых;

10) 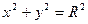, окружность.

Уравнения 1) – 10) называются каноническими уравнениями линий второго порядка.

Рассмотрим частные случаи уравнения (1) при  В=0.


1234Следующая ⇒
  

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.