Хелпикс

Главная

Контакты

Случайная статья



Окружность

⇐ ПредыдущаяСтр 2 из 4Следующая ⇒


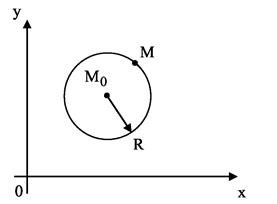
1. Окружность

Окружностью радиуса  R  с центром в точке 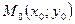  называется множество всех точек плоскости,  равноудаленных от точки  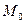 на расстояние  R .

Каноническое уравнение окружности имеет вид:

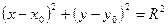                                           .                                   (2)

 

Уравнение окружности с центром в начале координат имеет вид:

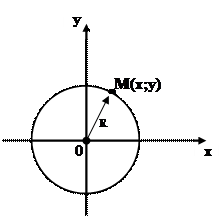
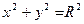                                                                                                  (3)

     
Рис.1.         Окружность с центром в точке
 
Рис.2.        Окружность  с центром в начале координат  

 

 


Пример 1.1.

Найти координаты центра и радиус окружности .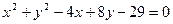

Решение.

Выделим полные квадраты: 

;

;   .

 

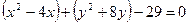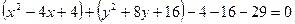Центр окружности находится в точке (2; -4),  радиус равен 7.

Пример 1.2.

Составить уравнение окружности, диаметром которой является отрезок, отсекаемый координатными осями от прямой .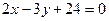

Решение.

Преобразуем общее уравнение прямой: 

; ; .

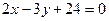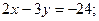
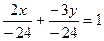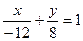Получили уравнение прямой в отрезках. Эта прямая пересекает координатные оси  в  точках А(-12; 0)  и  B(0; 8).

 

 

 


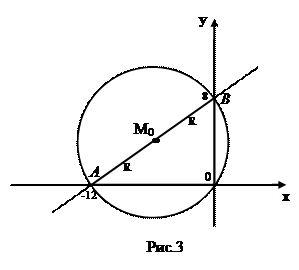
Центром окружности является точка 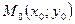 - середина отрезка АВ. Координаты этой точки найдем по формулам координат середины отрезка:

 ; .

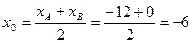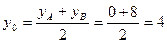Значит, .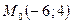

Радиус найдем как расстояние между точками 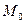 и  B:

.

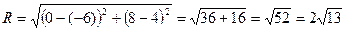Запишем уравнение окружности:     

.

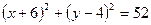Преобразовав это уравнение, мы получим общее уравнение окружности:

; .

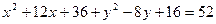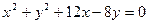Ответ: .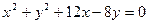

Задачи для самостоятельного решения:

Составить уравнение окружности в каждом из следующих случаев:

1. Центр окружности совпадает с началом координат и ее радиус .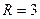

2. Центр окружности совпадает с точкой 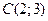 и ее радиус .

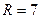3. Окружность проходит через точку 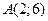и ее центр совпадает с точкой .

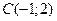4. Точк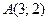и  и 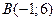 являются концами одного из диаметров окружности.

5. Центр окружности совпадает с началом координат и прямая 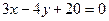 является касательной к окружности.

6. Центр окружности совпадает с точкой 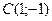 и прямая  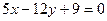является касательной к окружности.

7. Окружность проходит через точк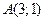и и 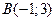, а ее центр лежит на прямой .

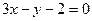8. Окружность проходит через три точки , , .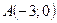

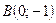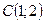9. Окружность касается прямых 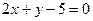, , 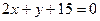причем одной из них – в точке .

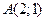10.  Окружность касается прямых 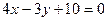, , 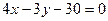центр лежит на прямой .


⇐ Предыдущая1234Следующая ⇒
  

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.