Теорема Ляпунова.. Задачи

Теорема Ляпунова.

Если Х₁, Х₂, …, Х_п, … - независимые случайные величины с одинаковым законом распределения, матожиданием a_i и дисперсией σ², то при неограниченном увеличении п закон распределения суммы 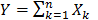неограниченно приближается к нормальному.

Тогда вероятность того, что случайная величина Y_n попадет в промежуток [α, β] выражается формулой

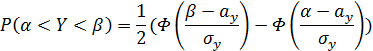
где 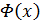- функция Лапласа 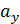и 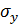- матожидание и среднеквадратическое отклонение величины .

Частным случаем является теорема Муавра-Лапласа.

Если производится n независимых опытов, в каждом из которых событие А появляется с вероятностью p, то справедливо соотношение

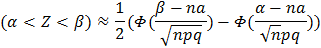
где Z – число появлений события А в n опытах, q=1-p.

Задачи

1. Средний вес клубня картофеля равен 120 г. Какова вероятность того, что наугад взятый клубень картофеля весит не более 360 г?

2. Среднее число молодых специалистов, ежегодно направляемых в аспирантуру, составляет 200 человек. Оценить вероятность того, что в данном году будет направлено в аспирантуру не более 220 молодых специалистов.

3. Оценить вероятность того, что при 3600 независимых подбрасываниях игрального кубика число появлений 6 очков будет не меньше 900.

4. Вероятность наступления некоторого события А в каждом из 1500 испытаний равна 0,2. Используя неравенство Чебышева, оценить вероятность того, что отклонение числа наступлений события А от математического ожидания будет более 40.

5. В рассматриваемом технологическом процессе в среднем 75% изделий имеет допуск %. С помощью неравенства Чебышева оценить вероятность того, что среди 2000 изделий к допуску % относится от 1450 до 1550 изделий включительно.

6. Известно, что 75% всей продукции, производимой заводом, высшего сорта. Оценить вероятность того, что число изделий высшего сорта среди 100000 изделий будет отличаться от математического ожидания этого числа не более чем на 1000 штук.

7. Вероятность наступления некоторого события А в каждом испытании равна 0,4. Определить вероятность того, что в 20000 испытаний отклонение частоты события А от вероятности его не превзойдет по абсолютной величине 0,01.

8. Сколько следует проверить деталей, чтобы с вероятностью не меньшей 0,95 можно было утверждать, что абсолютная величина отклонения частоты годных деталей от вероятности детали быть годной, равной 0,9, не превысит 0,01.

9. Случайная величина 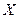имеет дисперсию 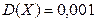. Какова вероятность того, что случайная величина 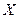отличается от 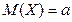более чем на 0,1?

10. Для случайной величины 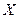известна дисперсия 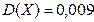и неравенство 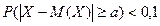. Найти число а.

11. Всхожесть семян некоторой культуры равна 0,75. Оценить вероятность того, что из посеянных 1000 семян число взошедших окажется от 700 до 800 включительно.

12. Найти вероятность того, что частота появления шестерки в 10000 независимых подбрасываниях игрального кубика отклоняется от вероятности появления шестерки по модулю меньше чем на 0,01.

13. При каком числе независимых испытаний вероятность выполнения неравенства 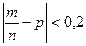превысит 0,96, если вероятность появления события в отдельном испытании .

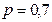14. Дисперсия каждой из 1000 независимых случайных величин 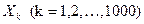равна 4. Оценить вероятность того, что отклонение средней арифметической этих величин от средней арифметической их математических ожиданий по модулю не превзойдет 0,1.

15. Всхожесть семян некоторого растения составляет 70%. Найти вероятность того, что при посеве 10000 семян отклонение доли взошедших семян от вероятности того, что взойдет каждое из них, не превзойдет по модулю 0,01.

16. Вероятность появления события А в каждом из 900 независимых испытаний равна 0,8. Найти вероятность того, что событий А произойдет: а) 750 раз; б) 710 раз.

17. Вероятность того, что электролампочка, изготовленная данным заводом, является бракованной, равна 0,02. Для контроля отобрано наугад 1000 лампочек. Оценить вероятность того, что частота бракованных лампочек в выборке отличается от вероятности 0,02 менее чем на 0,01.

18. Вероятность появления положительного результата в каждом из п опытов равна 0,9. Сколько нужно произвести опытов, чтобы с вероятностью 0,98 можно было ожидать, что не менее 150 опытов дадут положительный результат?

19. Вероятность появления события в каждом из 900 независимых испытаний равна 0,5. Найти такое положительное число 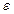, чтобы с вероятностью 0,77 модуль отклонения частоты появления события от его вероятности 0,5 не превышал .

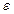20. Отдел технического контроля проверяет 475 изделий на брак. Вероятность того, что изделие бракованное, равна 0,05. Найти с вероятностью 0,95 границы, в которых будет заключено число т бракованных изделий среди проверенных.

21. Обследуется 500 изделий продукции, изготовленной на предприятии, где брак составляет 2%. Найти вероятности того, что: а) среди них окажется ровно 10 бракованных; б) число бракованных изделий будет в пределах от 10 до 20.

22. Оценить вероятность события , т.е. вероятность того, что частота наступления события А в 300 опытах отклоняется от вероятности события А не более чем на 0,01.

⇐ Предыдущая 1 2 34