
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Закон больших чисел и предельные теоремы
Закон больших чисел и предельные теоремы
Изучение статистических закономерностей позволило установить, что при некоторых условиях суммарное поведение большого количества случайных величин почти утрачивает случайный характер и становится закономерным (иначе говоря, случайные отклонения от некоторого среднего поведения взаимно погашаются). В частности, если влияние на сумму отдельных слагаемых является равномерно малым, закон распределения суммы приближается к нормальному. Математическая формулировка этого утверждения дается в группе теорем, называемой законом больших чисел.
Неравенства Маркова
Теорема. Если случайная величина 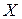 может принимать только неотрицательные значения и у нее есть математическое ожидание, то какова бы ни была величина
может принимать только неотрицательные значения и у нее есть математическое ожидание, то какова бы ни была величина 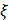 той же размерности, что и
той же размерности, что и  , всегда выполняется неравенствf
, всегда выполняется неравенствf
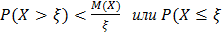 )≥1 -
)≥1 -  .
.
Пример 1. Средний срок службы мотора 4 года. Оценить снизу вероятность того, что данный мотор не прослужит 20 лет.
Решение. Пусть случайная величина  - срок службы мотора. Из условия задачи -
- срок службы мотора. Из условия задачи - 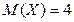 . Требуется оценить снизу вероятность
. Требуется оценить снизу вероятность  . Эту вероятность можно рассматривать как левую часть неравенства Маркова с
. Эту вероятность можно рассматривать как левую часть неравенства Маркова с  . Тогда
. Тогда  .
.
Пример 2. Сумма всех вкладов в некотором сберегательном банке составляет 2 млн. рублей, вероятность того, что случайно взятый вклад не превышает 10000 руб. равна 0.8. Что можно сказать о числе вкладчиков данного сберегательного банка?
Решение. Пусть  - величина случайно взятого вклада, а
- величина случайно взятого вклада, а  - число всех вкладчиков. Тогда из условия задачи следует, что
- число всех вкладчиков. Тогда из условия задачи следует, что 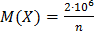 . Так как
. Так как  , то по неравенству Маркова получим
, то по неравенству Маркова получим  или
или 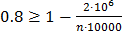 ,
,  ,
, 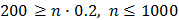 .
.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|