
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Теорема Бернулли
Теорема Бернулли
Теорема.Если в каждом из п независимых опытов вероятность р появления события А постоянна, то при достаточно большом числе испытаний вероятность того, что модуль отклонения относительной частоты появлений А в п опытах от р будет сколь угодно малым, как угодно близка к 1, то есть 
Замечание. Из теоремы Бернулли не следует, что  Речь идет лишь о вероятности того, что разность относительной частоты и вероятности по модулю может стать сколь угодно малой. Разница заключается в следующем: при обычной сходимости, рассматриваемой в математическом анализе, для всех п, начиная с некоторого значения, неравенство
Речь идет лишь о вероятности того, что разность относительной частоты и вероятности по модулю может стать сколь угодно малой. Разница заключается в следующем: при обычной сходимости, рассматриваемой в математическом анализе, для всех п, начиная с некоторого значения, неравенство  выполняется всегда; в нашем случае могут найтись такие значения п, при которых это неравенство неверно. Этот вид сходимости называют сходимостью по вероятности.
выполняется всегда; в нашем случае могут найтись такие значения п, при которых это неравенство неверно. Этот вид сходимости называют сходимостью по вероятности.
Пример 1. Пусть вероятность того, что покупателю обувного магазина необходимы туфли 41-ого размера, равна 0,15. Оценить границы процента покупателей среди 2000, побывавших в магазине, которым нужны такие туфли, если эти границы надо гарантировать с вероятностью 0,98.
Решение. Если т – число покупателей, которым нужны туфли 41-ого размера, то согласно теореме Бернулли, имеет место неравенство 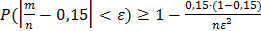 . Левая часть этого неравенства будет больше 0,98, если его правая часть больше этой вероятности. Мы приходим к неравенству
. Левая часть этого неравенства будет больше 0,98, если его правая часть больше этой вероятности. Мы приходим к неравенству 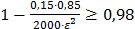 . Отсюда
. Отсюда 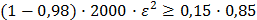 , откуда следует
, откуда следует 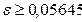 .
.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|