Неравенство Чебышева. Теорема Чебышева

Неравенство Чебышева

Теорема. Каково бы ни было для любой случайной величины 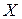, дисперсия которой конечна, имеет место неравенства Чебышева

> )< или .

Пример 1. Электростанция обслуживает сеть из 18000 ламп, вероятность включения каждой из них в зимний вечер равна 0,9. Оценить вероятность того, что число ламп, включенных в сеть зимним вечером, отличается от своего математического ожидания по абсолютной величине не менее чем на 200.

Решение. Так как число включенных ламп 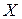- это случайная величина, распределенная по биномиальному закону, то математическое ожидание этой случайной величины равно произведению числа всех независимых испытаний (п=18000) на вероятность появления события в отдельном испытании (р=0,9), т.е. , . Здесь . Неравенство Чебышева дает оценку снизу вероятности выполнения неравенства , то есть

. Итак, .

Определение.Последовательность чисел называется равномерно ограниченной, если существует такая постоянная М, что для любого .

Теорема Чебышева

Если - последовательность попарно независимых случайных величин, у каждой из которых есть математическое ожидание и дисперсия , , 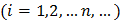причем дисперсии равномерно ограничены, то для любого положительного

Следствие.Если - последовательность независимых случайных величин, математические ожидания каждой из которых равны а, а дисперсии , то неравенство выше и утверждение теоремы принимают вид

, .

Отсюда видно, что среднее арифметическое значение величин , а это есть случайная величина, при большом числе как угодно мало отличается от постоянной величины а.

Пример 1. Для определения средней продолжительности горения электроламп в партии из 200 одинаковых ящиков было взято на выборку по одной лампе из каждого ящика. Оценить снизу вероятность того, что средняя продолжительность горения отобранных 200 электроламп отличается от средней продолжительности горения во всей партии по абсолютной величине меньше, чем на 5 часов, если известно, что среднее квадратичное отклонение продолжительности горения любой лампы в каждом ящике меньше 7 часов.

Решение. Пусть - продолжительность горения электролампы, взятой из i-го ящика. По условию задачи . Очевидно, что средняя продолжительность горения ламп в выборке , а средняя продолжительность горения ламп во всей партии . Оценим вероятность . Это есть левая часть неравенства из теоремы Чебышева. Так как - независимые случайные величины, то эта вероятность оценивается правой частью этого неравенства, где следует положить , , . Искомая вероятность .

⇐ Предыдущая 123 4 Следующая ⇒