Главная

Контакты

Случайная статья

• Автоматизация
• Антропология
• Археология
• Архитектура
• Биология
• Ботаника
• Бухгалтерия
• Военная наука
• Генетика
• География
• Геология
• Демография
• Деревообработка
• Журналистика
• Зоология
• Изобретательство
• Информатика
• Искусство
• История
• Кинематография
• Компьютеризация
• Косметика
• Кулинария
• Культура
• Лексикология
• Лингвистика
• Литература
• Логика
• Маркетинг
• Математика
• Материаловедение
• Медицина
• Менеджмент
• Металлургия
• Метрология
• Механика
• Музыка
• Науковедение
• Образование
• Охрана Труда
• Педагогика
• Полиграфия
• Политология
• Право
• Предпринимательство
• Приборостроение
• Программирование
• Производство
• Промышленность
• Психология
• Радиосвязь
• Религия
• Риторика
• Социология
• Спорт
• Стандартизация
• Статистика
• Строительство
• Технологии
• Торговля
• Транспорт
• Фармакология
• Физика
• Физиология
• Философия
• Финансы
• Химия
• Хозяйство
• Черчение
• Экология
• Экономика
• Электроника
• Электротехника
• Энергетика

Задание 13 № 746. Решение.. Другое решение.. Задание 13 № 1700. Решение.

52. Задание 13 № 746

Саша и Костя по очереди вычеркивают по одной цифре из числа 179284, пока не останется трехзначное число. Саша начинает, и его задача — сделать трехзначное число как можно меньше. а Костя хочет, чтобы трехзначное число было как можно больше. Может ли Саша получить число меньше 295, как бы не действовал Костя? Напишите свое решение.

Решение.

Для того, чтобы получить наименьшее число, Саша должен вычёркивать самую большую из имеющихся цифр, учитывая разряд, то есть, сначала он должен вычеркнуть цифру 9. Удобно показать решение в виде дерева.

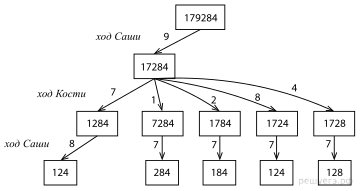
Другое решение.

Сначала Саша вычёркивает 9; если затем Костя вычёркивает 7, то Саша — 8, остаётся 124, а если Костя вычёркивает не 7, то Саша вычёркивает 7. Тогда остаётся одно из чисел 284, 184, 124 или 128. Все эти числа меньше 295.

Ответ: да, может.

53. Задание 13 № 1700

В мешке находится 31 белая перчатка и 32 чёрные перчатки. Перчатки достают из мешка парами. Если достали пару перчаток одного цвета, то в мешок кладут чёрную перчатку. Если достали пару перчаток разного цвета, то в мешок кладут белую перчатку. Какого цвета окажется перчатка, которая останется в мешке последней?

Решение.

На каждом шаге число белых перчаток либо не меняется, либо уменьшается на два. Так как число белых перчаток вначале было нечётным, после каждого шага их число также нечётно. Если последняя перчатка окажется чёрной,

то получится, что белых перчаток осталось 0. Это невозможно. Значит, останется белая перчатка.

Ответ: Белая перчатка.

54. Задание 13 № 1713

В мешке находится 21 белая перчатка и 26 чёрных перчаток. Перчатки достают из мешка парами. Если достали пару перчаток одного цвета, то в мешок кладут чёрную перчатку. Если достали пару перчаток разного цвета, то в мешок кладут белую перчатку. Какого цвета окажется перчатка, которая останется в мешке последней?

Решение.

На каждом шаге число белых перчаток либо не меняется, либо уменьшается на два. Так как число белых перчаток вначале было нечётным, после каждого шага их число также нечётно. Если последняя перчатка окажется чёрной,

то получится, что белых перчаток осталось 0. Это невозможно. Значит, останется белая перчатка.

Ответ: Белая перчатка.

55. Задание 13 № 1803

В мешке находится 22 белые перчатки и 25 чёрных перчаток. Перчатки достают из мешка парами. Если достали пару перчаток одного цвета, то в мешок кладут чёрную перчатку. Если достали пару перчаток разного цвета, то в мешок кладут белую перчатку. Какого цвета окажется перчатка, которая останется в мешке последней?

Решение.

На каждом шаге число белых перчаток либо не меняется, либо уменьшается на два. Так как число белых перчаток вначале было чётным, после каждого шага их число также чётно. Поэтому одна белая перчатка остаться в мешке не может. Значит, последней окажется чёрная перчатка.

Ответ: Черная перчатка.

56. Задание 13 № 1818

В мешке находится 24 белые перчатки и 20 чёрных перчаток. Перчатки достают из мешка парами. Если достали пару перчаток одного цвета, то в мешок кладут чёрную перчатку. Если достали пару перчаток разного цвета, то в мешок кладут белую перчатку. Какого цвета окажется перчатка, которая останется в мешке последней?

Решение.

На каждом шаге число белых перчаток либо не меняется, либо уменьшается на два. Так как число белых перчаток вначале было чётным, после каждого шага их число также чётно. Поэтому одна белая перчатка остаться в мешке не может. Значит, последней окажется чёрная перчатка.

Ответ: Черная перчатка.

57. Задание 13 № 1831

В мешке находится 27 белых перчаток и 29 чёрных перчаток. Перчатки достают из мешка парами. Если достали пару перчаток одного цвета, то в мешок кладут чёрную перчатку. Если достали пару перчаток разного цвета, то в мешок кладут белую перчатку. Какого цвета окажется перчатка, которая останется в мешке последней?

Решение.

На каждом шаге число белых перчаток либо не меняется, либо уменьшается на два. Так как число белых перчаток вначале было нечётным, после каждого шага их число также нечётно. Если последняя перчатка окажется чёрной,

то получится, что белых перчаток осталось 0. Это невозможно. Значит, останется белая перчатка.

Ответ: Белая перчатка.

58. Задание 13 № 1854

В мешке находится 33 белые перчатки и 30 чёрных перчаток. Перчатки достают из мешка парами. Если достали пару перчаток одного цвета, то в мешок кладут чёрную перчатку. Если достали пару перчаток разного цвета, то в мешок кладут белую перчатку. Какого цвета окажется перчатка, которая останется в мешке последней?

Решение.

На каждом шаге число белых перчаток либо не меняется, либо уменьшается на два. Так как число белых перчаток вначале было нечётным, после каждого шага их число также нечётно. Если последняя перчатка окажется чёрной,

то получится, что белых перчаток осталось 0. Это невозможно. Значит, останется белая перчатка.

Ответ: Белая перчатка.

59. Задание 13 № 1867

В мешке находится 28 белых перчаток и 31 чёрная перчатка. Перчатки достают из мешка парами. Если достали пару перчаток одного цвета, то в мешок кладут чёрную перчатку. Если достали пару перчаток разного цвета, то в мешок кладут белую перчатку. Какого цвета окажется перчатка, которая останется в мешке последней?

Решение.

На каждом шаге число белых перчаток либо не меняется, либо уменьшается на два. Так как число белых перчаток вначале было чётным, после каждого шага их число также чётно. Поэтому одна белая перчатка остаться в мешке не может. Значит, последней окажется чёрная перчатка.

Ответ: Черная перчатка.

60. Задание 13 № 1880

В мешке находится 30 белых перчаток и 34 чёрные перчатки. Перчатки достают из мешка парами. Если достали пару перчаток одного цвета, то в мешок кладут чёрную перчатку. Если достали пару перчаток разного цвета, то в мешок кладут белую перчатку. Какого цвета окажется перчатка, которая останется в мешке последней?

Решение.

На каждом шаге число белых перчаток либо не меняется, либо уменьшается на два. Так как число белых перчаток вначале было чётным, после каждого шага их число также чётно. Поэтому одна белая перчатка остаться в мешке не может. Значит, последней окажется чёрная перчатка.

Ответ: Черная перчатка.

61. Задание 13 № 1893

В мешке находится 32 белые перчатки и 28 чёрных перчаток. Перчатки достают из мешка парами. Если достали пару перчаток одного цвета, то в мешок кладут чёрную перчатку. Если достали пару перчаток разного цвета, то в мешок кладут белую перчатку. Какого цвета окажется перчатка, которая останется в мешке последней?

Решение.

На каждом шаге число белых перчаток либо не меняется, либо уменьшается на два. Так как число белых перчаток вначале было чётным, после каждого шага их число также чётно. Поэтому одна белая перчатка остаться в мешке не может. Значит, последней окажется чёрная перчатка.

Ответ: Черная перчатка.

62. Задание 13 № 1929

В мешке находится 29 белых перчаток и 31 чёрная перчатка. Перчатки достают из мешка парами. Если достали пару перчаток одного цвета, то в мешок кладут чёрную перчатку. Если достали пару перчаток разного цвета, то в мешок кладут белую перчатку. Какого цвета окажется перчатка, которая останется в мешке последней?

Решение.

На каждом шаге число белых перчаток либо не меняется, либо уменьшается на два. Так как число белых перчаток вначале было нечётным, после каждого шага их число также нечётно. Если последняя перчатка окажется чёрной,

то получится, что белых перчаток осталось 0. Это невозможно. Значит, останется белая перчатка.

Ответ: Белая перчатка.

63. Задание 13 № 1946

Саша, Петя и Вася играли в снежки. Первым кинул снежок Саша и попал в Петю. Каждый мальчик в ответ на каждый попавший в него снежок кидает два снежка (не обязательно в того, кто в него попал). Некоторые снежки ни в кого не попали. Всего было четыре попадания. Сколько снежков ни в кого не попало? Запишите решение и ответ.

Решение.

Всего было брошено 1 + 4 · 2 = 9 снежков. Значит, ни в кого не попало 9 − 4 = 5 снежков.

Ответ: 5 снежков.

64. Задание 13 № 1959

Катя, Вова и Женя играли в снежки. Первым кинул снежок Вова и попал в Женю. Каждый ребёнок в ответ на каждый попавший в него снежок кидает три снежка (не обязательно в того, кто в него попал). Некоторые снежки ни в кого не попали. Всего было четыре попадания. Сколько снежков ни в кого не попало?

Решение.

Всего было брошено 1 + 4 · 3 = 13 снежков.

Значит, ни в кого не попало 13 − 4 = 9 снежков.

Ответ: 9 снежков.

65. Задание 13 № 1972

Петя, Даша и Маша играли в снежки. Первым кинул снежок Петя и попал в Дашу. Каждый ребёнок в ответ на каждый попавший в него снежок кидает два снежка (не обязательно в того, кто в него попал). Некоторые снежки ни в кого не попали. Всего было пять попаданий. Сколько снежков ни в кого не попало?

Решение.

Всего было брошено 1 + 5 · 2 = 11 снежков.

Значит, ни в кого не попало 11 − 5 = 6 снежков.

Ответ: 6 снежков.

66. Задание 13 № 1985

Саша, Света и Юра играли в снежки. Первым кинул снежок Юра и попал в Сашу. Каждый ребёнок в ответ на каждый попавший в него снежок кидает три снежка (не обязательно в того, кто в него попал). Некоторые снежки ни в кого не попали. Всего было три попадания. Сколько снежков ни в кого не попало?

Решение.

Всего было брошено 1 + 3 · 3 = 10 снежков.

Значит, ни в кого не попало 10 − 3 = 7 снежков.

Ответ: 7 снежков.

67. Задание 13 № 1998

Маша, Вера и Егор играли в снежки. Первым кинул снежок Егор и попал в Машу. Каждый ребёнок в ответ на каждый попавший в него снежок кидает три снежка (не обязательно в того, кто в него попал). Некоторые снежки ни в кого не попали. Всего было пять попаданий. Сколько снежков ни в кого не попало? Запишите решение и ответ.

Решение.

Всего было брошено 1 + 5 · 3 = 16 снежков. Значит, ни в кого не попало 16 − 5 = 11 снежков.

Ответ: 11 снежков.

68. Задание 13 № 2011

Вася и Маша не умеют сокращать дроби. Они делают это неправильно. Вася думает, что нужно от числителя отнять 3, а от знаменателя отнять 2. Вася делает так: 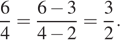Маша считает, что нужно от числителя отнять 2, а от знаменателя отнять 1. Маша делает так: 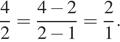Вася и Маша (не обязательно по очереди) двадцать раз «сократили» дробь по своим правилам и получили дробь со знаменателем 1995. Найдите числитель получившейся дроби. Запишите решение и ответ.

Решение.

После каждого «сокращения» данной дроби разность между знаменателем и числителем увеличивается на 1. Значит, после двадцати преобразований эта разность равна 2019 − 2018 + 20 = 21, поэтому числитель равен 1995 − 21 = 1974.

Ответ: 1974.

69. Задание 13 № 2024

Коля и Ира не умеют сокращать дроби. Они делают это неправильно. Коля думает, что нужно от числителя отнять 2, а от знаменателя отнять 1. Коля делает так: 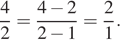Ира считает, что нужно от числителя отнять 4, а от знаменателя отнять 3. Ира делает так: Коля и Ира (не обязательно по очереди) двадцать раз «сократили» дробь по своим правилам и получили дробь с числителем 1966. Найдите знаменатель получившейся дроби. Запишите решение и ответ.

Решение.

После каждого «сокращения» данной дроби разность между знаменателем и числителем увеличивается на 1. Значит, после двадцати преобразований эта разность равна 2019 − 2018 + 20 = 21, поэтому знаменатель равен 1966 + 21 = 1987.

Ответ: 1987.

70. Задание 13 № 2039

Олег и Аня не умеют сокращать дроби. Они делают это неправильно. Олег думает, что нужно от числителя отнять 4, а от знаменателя отнять 3. Олег делает так: Аня считает, что нужно от числителя отнять 3, а от знаменателя отнять 2. Аня делает так: 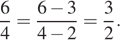Олег и Аня (не обязательно по очереди) тридцать раз «сократили» дробь по своим правилам и получили дробь со знаменателем 1952. Найдите числитель получившейся дроби. Запишите решение и ответ.

Решение.

После каждого «сокращения» данной дроби разность между знаменателем и числителем увеличивается на 1. Значит, после тридцати преобразований эта разность равна 2019 − 2018 + 30 = 31, поэтому числитель равен 1952 − 31 = 1921.

Ответ: 1921.

71. Задание 13 № 2058

Ваня и Аня не умеют сокращать дроби. Они делают это неправильно. Ваня думает, что нужно от числителя отнять 2, а от знаменателя отнять 3. Ваня делает так: 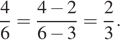Аня считает, что нужно от числителя отнять 1, а от знаменателя отнять 2. Аня делает так: 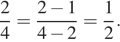Ваня и Аня (не обязательно по очереди) двадцать раз «сократили» дробь по своим правилам и получили дробь с числителем 1992. Найдите знаменатель получившейся дроби. Запишите решение и ответ.

Решение.

После каждого «сокращения» данной дроби разность между знаменателем и числителем увеличивается на 1. Значит, после двадцати преобразований эта разность равна 2019 − 2018 + 20 = 21, поэтому знаменатель равен 1992 − 21 = 1971.

Ответ: 1971.

72. Задание 13 № 2071

Коля и Оля не умеют сокращать дроби. Они делают это неправильно. Коля думает,что нужно от числителя отнять 3, а от знаменателя отнять 4. Коля делает так: 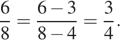Оля считает, что нужно от числителя отнять 2, а от знаменателя отнять 3. Оля делает так: 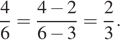Коля и Оля (не обязательно по очереди) пятнадцать раз «сократили» дробь по своим правилам и получили дробь со знаменателем 1968. Найдите числитель получившейся дроби. Запишите решение и ответ.

Решение.

После каждого «сокращения» данной дроби разность между знаменателем и числителем увеличивается на 1. Значит, после пятнадцати преобразований эта разность равна 2019 − 2018 + 15 = 16, поэтому числитель равен 1968 + 16 = 1984.

Ответ: 1984.

73. Задание 13 № 7566

В мешке находятся 29 белых перчаток и 31 чёрная перчатка. Перчатки достают из мешка парами. Если достали пару перчаток одного цвета, то в мешок кладут чёрную перчатку. Если достали пару перчаток разного цвета, то в мешок кладут белую перчатку. Какого цвета окажется перчатка, которая останется в мешке последней? Запишите решение и ответ.

Решение.

На каждом шаге число белых перчаток либо не меняется, либо уменьшается на два. Так как число белых перчаток вначале было нечётным, после каждого шага их число также нечётно. Если последняя перчатка окажется чёрной, то получится, что белых перчаток осталось 0. Это невозможно. Значит, останется белая перчатка.

Ответ: белая перчатка.

74. Задание 13 № 7579

В мешке находятся 32 белые перчатки и 28 чёрных перчаток. Перчатки достают из мешка парами. Если достали пару перчаток одного цвета, то в мешок кладут чёрную перчатку. Если достали пару перчаток разного цвета, то в мешок кладут белую перчатку. Какого цвета окажется перчатка, которая останется в мешке последней? Запишите решение и ответ.

Решение.

В мешке находятся 32 белые перчатки и 28 чёрных перчаток. Перчатки достают из мешка парами. Если достали пару перчаток одного цвета, то в мешок кладут чёрную перчатку. Если достали пару перчаток разного цвета, то в мешок кладут белую перчатку. Какого цвета окажется перчатка, которая останется в мешке последней? Запишите решение и ответ.

Ответ: чёрная перчатка.

75. Задание 13 № 7773

В погребе хранилось несколько головок сыра. Ночью пришли мышки и съели 10 головок сыра, причём все съели поровну. Следующей ночью пришли не все мышки, а только 11, и доели оставшийся сыр, но каждая мышка съела в два раза меньше сыра, чем накануне. Сколько головок сыра хранилось в погребе? Запишите решение и ответ.

Решение.

Пусть в первую ночь мышей было х. Каждая съела головок сыра. Во вторую ночь мышей было 11, а головок сыра осталось у. Каждая мышь съела 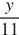головок сыра. По условию, 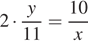. Значит, 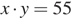. Поскольку х и у — натуральные числа, причём х > 11, то х = 55, а у = 1. Сначала в погребе было 11 головок сыра.

Допускается другая последовательность действий и рассуждений, обоснованно приводящая к верному ответу.

Ответ: 11 головок сыра.