Задание 13 № 420. Решение.. Задание 13 № 421. Решение.. Задание 13 № 422. Решение.. Задание 13 № 423. Решение.. Задание 13 № 472. Решение.. Задание 13 № 485. Решение.. Задание 13 № 602. Решение.. Задание 13 № 615. Решение.. Задание 13 № 628. Решение.. Зад

37. Задание 13 № 420

Вася написал на доске пример на умножение двух двузначных чисел, а затем заменил в нем все цифры на буквы, причём одинаковые цифры — на одинаковые буквы, а разные — на разные. В итоге у него получилось АБ · ВГ = ДДЕЕ. Докажите, что он где-то ошибся.

Решение.

Число слева не делится на 11, а справа — делится (при делении получается число Д0Е).

38. Задание 13 № 421

Сколько имеется четырёхзначных чисел, которые делятся на 45, а две средние цифры у них 97?

Решение.

Чтобы число делилось на 45 оно должно делиться на 9 и на 5. Число делится на 5, если оно оканчивается на 0 или 5. Число делится на 9, если сумма всех цифр числа делится на 9. Учитывая эти ограничения, получим, что чисел, удовлетворяющих условиям задачи два: 2970 и 6975.

39. Задание 13 № 422

К числу 15 припишите слева и справа по одной цифре так, чтобы полученное число делилось на 15.

Решение.

Результатом могут быть числа: 1155, 3150, 4155, 6150, 7155, 9150.

40. Задание 13 № 423

Найти наименьшее натуральное число, делящееся на 36, в записи которого встречаются все 10 цифр.

Решение.

Чтобы число делилось на 36, оно должно делится на 9 и 4 одновременно. Для делимости на 4 достаточно, чтобы две последних цифры делились на 4, а для 9 — сумма цифр делилось на 9. Так как нужно найти наименьшее число, используя все 10 цифр, получаем 1023456789, но оно не соответствует делимости на 4. Пробуем менять местами две последние цифры, получаем 1023456798 — не подходит. Так далее до 4 цифр — 1023457896.

Ответ: 1023457896.

41. Задание 13 № 472

Тренер купил несколько мячей, скакалок, обручей и заплатил за все покупки 1690 рублей. Скакалка стоит 260 рублей, обруч — 130 рублей, мяч — 100 рублей. Сколько мячей, скакалок и обручей купил тренер? Ответ поясните.

Решение.

Из условия следует, что тренер купил как минимум одну скакалку, один обруч и один мяч. Числа 1690, 260 и 130 кратны 13. Число 100 не кратно 13, значит, общая стоимость мячей должна быть кратна 13. Предположим, что мячей 13. Тогда 1690 − 13 · 100= 390 — столько денег останется на покупку скакалок и обручей. Получаем, что 390 — сумма при покупке 1 скакалки и 1 обруча.

Ответ: 13 мячей, 1 скакалка и 1 обруч.

42. Задание 13 № 485

Тренер купил несколько мячей, скакалок, обручей и заплатил за все покупки 1540 рублей. Скакалка стоит 330 рублей, обруч — 220 рублей, мяч — 90 рублей. Сколько мячей, скакалок и обручей купил тренер? Ответ поясните.

Решение.

Из условия следует, что тренер купил как минимум одну скакалку, один обруч и один мяч. Числа 1540, 330 и 220 кратны 11. Число 90 не кратно 11, значит, общая стоимость мячей должна быть кратна 11. Предположим, что мячей 11. Тогда 1540 − 11 · 90= 550 — столько денег останется на покупку скакалок и обручей. Получаем, что 550 — сумма при покупке 1 скакалки и 1 обруча.

Ответ: 11 мячей, 1 скакалка и 1 обруч.

43. Задание 13 № 602

Задумали двузначное число. Когда это число умножили на произведение его цифр, получили 255. Какое число задумали? Напишите свое решение.

Решение.

Разложим число 255 на простые множители: 255 = 3 · 5 · 17. Отсюда следует, что задуманное число делится на 17. Тогда оно может равняться 17, 34, 51, 68 или 85. Из этих чисел только 51 и 85 имеют в своей записи цифлу 5. Проверим их:

51 · 5 · 1 = 255,

85 · 5 · 8=3400.

Допускается другая последовательность действий и рассуждений, обоснованно приводящая к верному ответу.

Ответ: 51.

44. Задание 13 № 615

Задумали двузначное число. Когда это число умножили на произведение его цифр, получили 744. Какое число задумали. Напишите свое решение.

Решение.

Разложим число 744 на простые множители: 744 = 2 · 2 · 2 · 3 · 31. Отсюда следует, что задуманное число делится на 31. Тогда оно может равняться 31, 62, 93. Проверим каждое из них:

31 · 3 = 93,

62 · 12 = 744,

93 · 27 = 2511.

Допускается другая последовательность действий и рассуждений, обоснованно приводящая к верному ответу.

Ответ: 62.

45. Задание 13 № 628

Задумали двузначное число. Когда это число умножили на произведение его цифр, получили 819. Какое число задумали. Напишите свое решение.

Решение.

Разложим число 819 на простые множители: 819 = 3 · 3 · 7 · 13. Отсюда следует, что задуманное число делится на 13. Тогда оно может равняться 13, 26, 39, 52, 65, 78. Так как 819 нечетное, в задуманном числе только нечетные цифры. Значит, оно может равняться 13, 39 или 91. Проверим эти числа:

13 · 3 = 39,

39 · 27 = 1053,

91 · 9 = 819.

Допускается другая последовательность действий и рассуждений, обоснованно приводящая к верному ответу.

Ответ: 91.

46. Задание 13 № 641

Задумали двузначное число. Когда это число умножили на произведение его цифр, получили 312. Какое число задумали. Напишите свое решение.

Решение.

Разложим число 312 на простые множители: 312 = 2 · 2 · 2 · 3 · 13. Отсюда следует, что задуманное число делится на 13. Тогда оно может равняться 13, 26, 39, 52, 65, 78, 91. Проверим каждое из них:

13 · 3 = 39,

26 · 12 = 312.

Допускается другая последовательность действий и рассуждений, обоснованно приводящая к верному ответу.

Ответ: 26.

47. Задание 13 № 654

Задумали двузначное число. Когда это число умножили на произведение его цифр, получилось 912. Какое число задумали? Напишите своё решение.

Решение.

Разложим число 912 на простые множители: 912 = 2 · 2 · 2 · 2 · 3 · 19. Отсюда следует, что задуманное число делится на 19. Тогда оно может равняться 19, 38, 57, 76 или 95. Так как число 912 чётное, задуманное число содержит хотя бы одну чётную цифру. Значит, оно может равняться 38 или 76. Проверим эти числа:

38 · 24 = 912,

76 · 42 = 3192.

Ответ: 38.

48. Задание 13 № 667

Задумали двузначное число, которое делится на 15. Когда к этому числу приписали справа его последнюю цифру, получилось трёхзначное число, которое при делении на 9 даёт остаток 3. Какое число задумали? Напишите своё решение.

Решение.

Из всех двузначных чисел кратны 15 только 15, 30, 45, 60, 75, 90. Если приписать к ним справа их последнюю цифру, то мы получим ряд: 155, 300, 455, 600, 755, 900. Поделим каждое из них, кроме последнего, и найдем получившийся остаток:

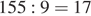(ост. 2)

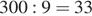(ост. 3)

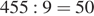(ост. 5)

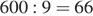(ост. 6)

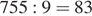(ост. 8)

Ответ: 30.

49. Задание 13 № 680

Задумали двузначное число, которое делится на 15. Когда к этому числу приписали справа его последнюю цифру, получилось трёхзначное число, которое при делении на 9 даёт остаток 6. Какое число задумали? Напишите своё решение.

Решение.

Задуманное число делится на 3. Полученное трехзначное число тоже делится на 3. Значит, приписанная цифра делится на 3. Эта цифра делится на 5, поскольку задуманное число делится на 5. Значит, эта цифра равна 0.

Выпишем все двузначные числа, которые оканчиваются нулем и делятся на 15: 30, 60, 90.

Проверим их:

300 при делении на 9 дает остаток 3,

600 при делении на 9 дает остаток 6,

900 делится 9 без остатка.

Ответ: 60.

50. Задание 13 № 694

Задумано двузначно число, которое делится на 5. К нему справа приписали это же число еще раз. Оказалось, что получившееся четырехзначное число делится на 11. Какое число задумали? Напишите свое решение.

Решение.

Пусть x — задуманное число, тогда полученное четырехзначное число равно 101x. Оно, по условию, делится на 11. Отсюда следует, что x делится на 11, так как число 101 простое. Поскольку задуманное двузначное число делится на 5 и 11, оно равно 55.

Ответ: 55.

51. Задание 13 № 733

Саша и Костя по очереди вычеркивают по одной цифре из числа 456127, пока не останется трехзначное число. Саша начинает, и его задача — сделать трехзначное число как можно меньше. а Костя хочет, чтобы трехзначное число было как можно больше. Может ли Саша получить число меньше 445, как бы не действовал Костя? Напишите свое решение.

Решение.

Для того, чтобы получить наименьшее число, Саша должен вычёркивать самую большую из имеющихся цифр, учитывая разряд, то есть, сначала он должен вычеркнуть цифру 6. Удобно показать решение в виде дерева.

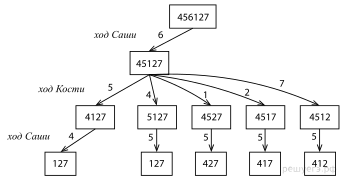
Другое решение.

Сначала Саша вычёркивает 6; если затем Костя вычёркивает 5, то Саша — 4, остаётся 127, а если Костя вычёркивает не 5, то Саша вычёркивает 5. Тогда остаётся одно из чисел 127, 427, 417 или 412. Все эти числа меньше 445.

Ответ: да, может.

⇐ Предыдущая 1 234 Следующая ⇒