
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Задача 2. Пример 1.. Комментарий.. Оценка эксперта: 0 баллов.. Пример 2.
Задача 2
В трапеции  боковая сторона
боковая сторона 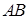 перпендикулярна основаниям.
перпендикулярна основаниям.
Из точки 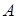 на сторону
на сторону 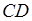 опустили перпендикуляр
опустили перпендикуляр  . На стороне
. На стороне 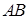 отмечена точка
отмечена точка  так, что прямые
так, что прямые 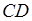 и
и  перпендикулярны.
перпендикулярны.
а) Докажите, что прямые 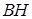 и
и 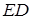 параллельны.
параллельны.
б) Найдите отношение 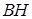 к
к 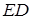 , если
, если 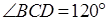 .
.
Решение.
а) Поскольку
 ,
около четырёхугольников ,
около четырёхугольников 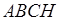 и и 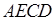 можно описать окружности (рис. 1).
Значит, можно описать окружности (рис. 1).
Значит,
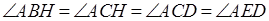 ,
то есть прямые ,
то есть прямые 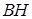 и и 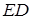 параллельны. параллельны.
| 
|
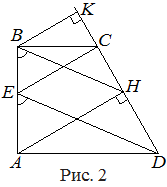
б) Опустим из точки 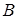 перпендикуляр перпендикуляр 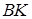 на прямую на прямую 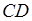 (рис. 2). Стороны (рис. 2). Стороны 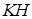 и и 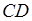 треугольников треугольников 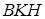 и и 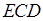 лежат на одной прямой, а стороны лежат на одной прямой, а стороны 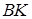 и и 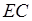 , , 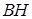 и и 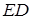 попарно параллельны. Значит, треугольники попарно параллельны. Значит, треугольники 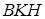 и и 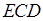 подобны.
Поскольку подобны.
Поскольку
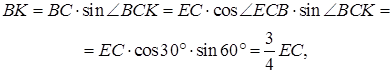
| 
|
коэффициент подобия равен  . Значит,
. Значит,
 .
.
Ответ: б) 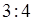 .
.
Пример 1.
В трапеции  боковая сторона
боковая сторона 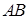 перпендикулярна основаниям.
перпендикулярна основаниям.
Из точки 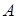 на сторону
на сторону 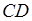 опустили перпендикуляр
опустили перпендикуляр  . На стороне
. На стороне 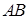 отмечена точка
отмечена точка  так, что прямые
так, что прямые 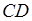 и
и  перпендикулярны.
перпендикулярны.
а) Докажите, что прямые 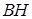 и
и 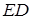 параллельны.
параллельны.
б) Найдите отношение 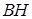 к
к 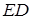 , если
, если 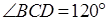 .
.
Ответ: б) 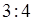 .
.

Комментарий.
Имеется попытка доказательства утверждения пункта а. Логическая ошибка содержится в записи 5) – при вычислении угла 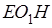 :
:  . Замена угла
. Замена угла 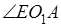 углом
углом 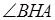 возможна только при условии параллельности прямых
возможна только при условии параллельности прямых 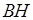 и
и 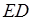 , а как раз это и требовалось доказать.
, а как раз это и требовалось доказать.
Оценка эксперта: 0 баллов.
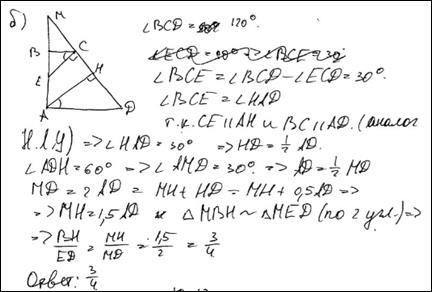
Пример 2.
В трапеции  боковая сторона
боковая сторона 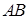 перпендикулярна основаниям.
перпендикулярна основаниям.
Из точки 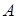 на сторону
на сторону 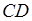 опустили перпендикуляр
опустили перпендикуляр  . На стороне
. На стороне 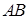 отмечена точка
отмечена точка  так, что прямые
так, что прямые 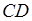 и
и  перпендикулярны.
перпендикулярны.
а) Докажите, что прямые 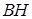 и
и 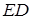 параллельны.
параллельны.
б) Найдите отношение 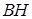 к
к 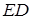 , если
, если 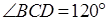 .
.
Ответ: б) 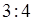 .
.

|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|