Хелпикс

Главная

Контакты

Случайная статья



Задача 16 (демонстрационный вариант 2020 г.).

Стр 1 из 4Следующая ⇒


Задача 16 (демонстрационный вариант 2020 г.).

Задача 1

Две окружности касаются внешним образом в точке 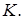 Прямая  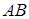касается первой окружности в точке 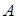, а второй — в точке  Прямая 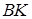 пересекает первую окружность в точке  прямая 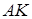 пересекает вторую окружность
в точке

а) Докажите, что прямые AD и BC параллельны.

б) Найдите площадь треугольника , если известно, что радиусы окружностей равны 4 и 1.

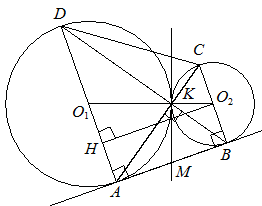
Решение. а) Обозначим центры окружностей  и 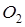 соответственно. Пусть общая касательная, проведённая
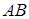к окружностям в точке  пересекает  в точке  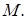По свойству касательных, проведённых из одной точки,  
и 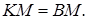 Треугольник AKB, у которого медиана равна половине стороны,
к которой она проведена, прямоугольный.

Вписанный угол 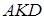 прямой, поэтому он опирается на диаметр  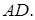Значит,  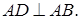Аналогично, получаем, что  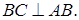Следовательно, прямые AD и BC параллельны.

б) Пусть, для определённости, первая окружность имеет радиус 4, а вторая — радиус 1.

Треугольники  и 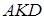 подобны, 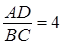. Пусть  тогда

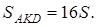
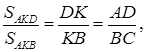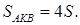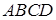У треугольников AKD и AKB общая высота, следовательно,  то есть  Аналогично,  Площадь трапеции  равна .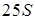

Вычислим площадь трапеции ABCD. Проведём к  перпендикуляр  равный высоте трапеции, и найдём его из прямоугольного треугольника :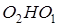

.

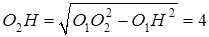Тогда

.

Следовательно, 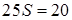, откуда  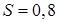и

Ответ: 3,2.


1234Следующая ⇒
  

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.