Ньютон - Рихман заңы.

2.Ньютон - Рихман заңы.

Мөлшерлілік теориясы дифференциалдық теңдеу жоқ болған кезде, яғни қазіргі процесті сипаттау қолданылады. Амалсыз конвекция шарттарында жылу беру коэффициентінің мәні кем дегенде алты тәуелсіз айнымалының функциясы бола алады: салмақ жылдамдығы u, кг/(м²×с); ұзындық мөлшері l; тұтқырлық

m,кг/(м×с);жылусыйымдылық С, Дж/(кг×К) және тығыздық r, кг/м³, жылуөткізгіштік l, Вт/(м×К).

Тәжірибеде анықталғандай a -ның Вт/(м²×К) бағыныштылығын a-дан бастап 6 ауыспалы және сандарды 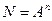(мұндағы А=10) тәжірибеден өткізу керек,мысалға А = 10; n — бағынбайтын ауыспалы сандар.Бұдан тәжірибелер саны бір миллионға тең екенін көреміз, бұл нақты сан болмайды. Мөлшерлілік теорияларды қолдану тәуелсәз ауыспалыларды қысқартуға мүмкіндік береді . Амалсыз конвекция шарттарында жылу беру коэффициенті функция болып келеді

a = a(u, l, m, С, r, l). (4.42)

Толық дифференциал a мынаған тең:

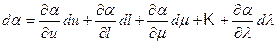. . (4.43)

Келесі өлшемсіздерге ( салыстырмалымен ) өту үшін тұрақты о-ден басқа өзгергіш мөлшерлер қажетті болады. Aлынған теңдеуді a-ға бөлеміз және бір уақытта сәйкес белгілерге (l/l; u/u; m/m т.с.с ) бөлеміз және көбейтеміз, сонда

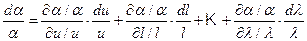. . (4.44)

Жеке туынды арақатынастарын тұрақты деп есептейміз :

; ; …; ,

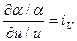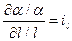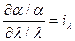Сонда мынаны аламыз

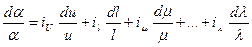. . (4.45)

Алынғанды интегралдаймыз :

ln a=i_u ln u+i_l ln l+…+i_l ln l+ln C₀ (4.46)

Потенциалдасақ,мынаны аламыз

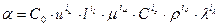. . (4.47)

Қажетті шартпен алынған жалпы шешім тұрақты С₀ немесе оның кері мөлшері болуы керек :

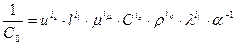. . (4.48)

Бұл теңдеу бірліктер жүйесіне тәуелді болмайды , ал С₀ өлшемсіз болғандықтан, барлық өлшеулердің бірліктері ( оңңан ) «0» дәрежеге теңдеуге кіреді, яғни мөлшерліліктің жоғына байланысты

⇐ Предыдущая 1 2 3 456 7 8 9 10 Следующая ⇒