Решение задачи 6. Решение задачи 7

Решение задачи 6

Точки А, В, С и D не лежат в одной плоскости (Рис. 11.).

а) Могут ли какие-то три из них лежать на одной прямой?

б) Могут ли прямые АВ и СD пересекаться?

Рис. 11.

Решение:

а) Предположим, что любые три точки, например, А, В, С лежат на одной прямой. Тогда через эту прямую и точку Dпроходит плоскость, и все 4 точки лежат в этой плоскости, что противоречит условию;

Ответ: нет.

б) Нет, так как через пересекающиеся прямые можно провести плоскость, а тогда, в этой плоскости содержатся все 4 точки, что противоречит условию.

Ответ: нет.

Решение задачи 7

а) Верно ли, что любые 3 точки лежат в одной плоскости?

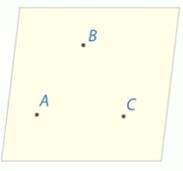
Рис. 12.

Через 3 точки, если они не лежат на одной прямой, можно провести плоскость, и притом только одну, в силу аксиомы А1.

Ответ: да.

б) Верно ли, что любые 4 точки лежат в одной плоскости?

Рис. 13.

Через 3 точки можно провести плоскость, а 4 точку можно взять и в этой плоскости, и вне нее. Значит, ответ отрицательный.

Ответ: нет.

в) Верно ли, что любые 4 точки не лежат в одной плоскости?

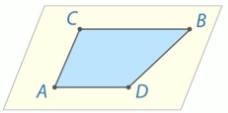
Рис. 14.

Приведем конкретный пример. Рассмотрим плоский четырехугольник, в плоскости этого четырехугольника лежат 4 точки. Итак, ответ на этот вопрос отрицательный, нет.

Ответ: нет.

г) Верно ли, что через любые 3 точки проходит плоскость, и притом только одна?

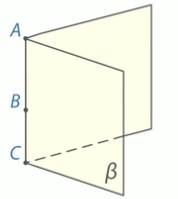
Рис. 15.

Приведем пример. Возьмем 3 точки А, В, С, лежащие на одной прямой. Через них можно провести плоскость , плоскость 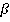. Через 3 точки, лежащие на одной прямой, можно провести бесконечное количество плоскостей.

Ответ: нет

⇐ Предыдущая 1 2 3 45