Теорема 1. Теорема 2. Решение задачи 1. Задача 1.

⇐ ПредыдущаяСтр 2 из 5Следующая ⇒

Теорема 1

Через прямую и не лежащую на ней точку проходит плоскость, и притом только одна.

Иллюстрация теоремы 1. (Рис. 4.)

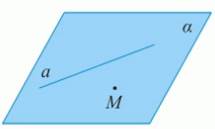
Рис. 4.

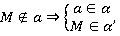
единственная

Теорема 2

Через две пересекающиеся прямые проходит плоскость, и притом только одна.

Иллюстрация теоремы 2. (Рис. 5.)

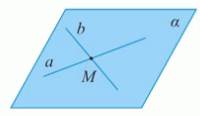
Рис. 5.

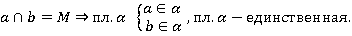
Решение задачи 1

Задача 1.

Даны две прямые, которые пересекаются в точке М. Докажите, что все прямые, не проходящие через точку М и пересекающие данные прямые, лежат в одной плоскости (Рис. 6.).

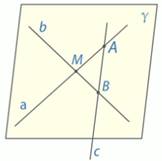
Рис. 6.

Решение:

Нам даны две прямые а и b, которые пересекаются в некоторой точке М. Возьмем произвольную прямую с, которая не проходит через точку М, но пересекает исходные прямые а и b в точках А, В, соответственно.

Через две пересекающиеся прямые проходит плоскость, и притом только одна, согласно 2 теореме. Значит через пересекающиеся прямые а и b проходит единственная плоскость, обозначим ее .

Две разные точки А и В прямой с принадлежат плоскости . А из того, что две точки прямой принадлежат плоскости, вытекает, что все точки прямой принадлежат плоскости, т.е. вся прямая лежит в плоскости. Значит, прямая с принадлежит этой плоскости.

Таким образом, мы доказали, что все прямые, пересекающие А и В, но не проходящие через М, лежат в одной плоскости.

⇐ Предыдущая 123 4 5 Следующая ⇒