Решение задачи 2. Решение задачи 3

Решение задачи 2

Три данные точки соединены попарно отрезками. Докажите, что все отрезки лежат в одной плоскости.

Решение:

Пусть нам даны три точки: А, В, и С. Нужно доказать, что отрезки АВ, ВС, СА лежат в одной плоскости (Рис. 7.).

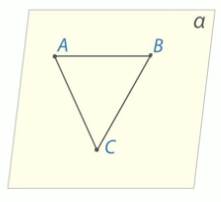
Рис. 7.

Если точка С лежит на прямой АВ, то ответ очевиден. Предположим, что точка С не принадлежит прямой АВ. Тогда через три точки A, B, C, не лежащие на одной прямой, проходит плоскость, и притом только одна, в силу аксиомы 1. Обозначим эту плоскость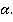

Прямая АВ целиком лежит в плоскости , потому что две ее точки лежат в этой плоскости. Но, значит, и отрезок АВ лежит в плоскости .

Аналогично и с другими отрезками. Прямая ВС лежит в плоскости , потому что две ее точки В и С лежат в плоскости 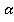, значит, и отрезок ВС лежит в плоскости .

И аналогично, отрезок АС лежит в плоскости . Что и требовалось доказать.

Решение задачи 3

Две смежные вершины и точка пересечения диагоналей параллелограмма лежат в плоскости . Лежат ли 2 другие вершины параллелограмма в плоскости ?

Решение:

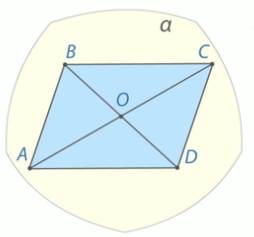
Рис. 8.

Пусть дан параллелограмм АВСD. Известно: точка А, точка В, точка О – точка пересечения диагоналей, лежат в плоскости . Нужно проверить, лежат ли вершины С и D лежат также в этой плоскости.

Через три точки А, В и О проходит плоскость, и притом только одна. Это плоскость . Прямая АО целиком лежит в этой плоскости, потому что две ее точки лежат в плоскости. Значит, точка С, точка прямой АО, лежит в плоскости .

Аналогично, прямая ВО целиком лежит в плоскости , значит, точка D этой прямой тоже лежит в плоскости .

Ответ: Да, вершины С и D лежат в плоскости .

⇐ Предыдущая 1 234 5 Следующая ⇒