Перпендикулярные прямые

Перпендикулярные прямые

Две прямые называются перпендикулярными, если они пересекаются пол прямым углом.

Перпендикуляром к данной прямой называется отрезок прямой, перпендикулярной данной, имеющий концом их точку пересечения. Этот конец отрезка называется основанием перпендикуляра.

Теорема: Через каждую точку прямой можно провести перпендикулярную ей прямую и притом только одну.

Доказательство:

Пусть АÎа. Докажем, что через точку А можно провести b^a. Обозначим через а₁ одну из полупрямых прямой а с началом в точке А. Отложим от полупрямой а₁ угол Ð(а₁b)=90°. Тогда прямая содержащая полупрямую b будет перпендикулярна прямой а.

Докажем единственность. Допустим, что существует другая прямая, также проходящая через точку А перпендикулярно прямой а. Обозначим через с полупрямую этой прямой, лежащую в одной полуплоскости с лучом b. Получим противоречие аксиоме, что в данную полуплоскость от данной полупрямой можно отложить только один угол с заданной градусной мерой. Таким образом, перпендикуляр единственен.

Теорема: Через точку, не лежащую на прямой, можно провести перпендикуляр к этой прямой и только один.

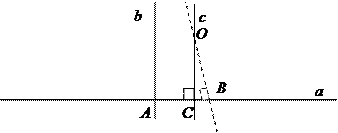Доказательство: Покажем, что такой перпендикуляр существует, т.е. его можно построить. Возьмем на прямой а некоторую точку А. Через нее проведем перпендикуляр к прямой а (прямая b). Через точку О проведем прямую, параллельную прямой b (прямая с). Тогда с^а.

Докажем единственность. Допустим, что через точку О можно провести еще хотя бы один перпендикуляр к прямой а - ОВ. В этом случае мы получим треугольник DОВС с двумя прямыми углами, что невозможно. Следовательно, перпендикуляр единственен.

Длина перпендикуляра, опущенного из данной точки на прямую, называется расстоянием от точки до прямой.

Расстоянием между параллельными прямыми называется расстояние от какой-либо точки взятой на на одной из параллельных прямых, до другой прямой.

Наклонной к данной прямой называется отрезок, имеющий концами точки пересечения этой прямой с данной и перпендикуляром к данной прямой.

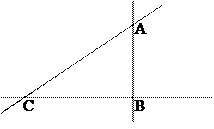АС – наклонная

АВ – перпендикуляр

ВС – проекция

С – основание наклонной

Если к прямой из одной точки проведены наклонная и перпендикуляр, то

1) Любая наклонная больше перпендикуляра

2) Равные наклонные имеют равные проекции

3) Из двух наклонных больше та, у которой проекция больше.

(следует из теоремы Пифагора – доказать самостоятельно)

Прямую, проходящую через середину отрезка перпендикулярно к нему называют серединным перпендикуляром.

Теорема: Любая точка, лежащая на серединном перпендикуляре к отрезку одинаково удалена от концов этого отрезка.

Доказательство: самостоятельно

⇐ Предыдущая 1 2 34