Пример 1-10.

Пример 1-10.

1) Функции sin х и 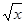имеют тип R®R, т.е. отображают одно и то же множество в себя. Поэтому их композиция возможна в произвольном порядке и дает функци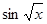и и 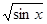. Заметим, что области определения их различны: первая функция определена на положительной полуоси; вторая функция определена на множестве отрезков 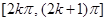, где k = 0, ±1, ±2 ... Таким образом, область определения композиции может быть уже областей определения обеих исходных функций и даже оказаться пустой.

2) Множество К = {k₁, …, k_m} команд ЭВМ отображается в машинные коды этой ЭВМ, т. е. в натуральные числа. Кодирующая функция имеет тип К®N. С помощью суперпозиции этой функции и арифметических функций оказываются возможными арифметические действия над командами (которые сами по себе числами не являются!), т.е. функции вида 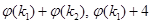и т.д.

3) В функции f₁(x₁, x₂, x₃) = x₁+2x₂+7x₃переименование x₃ в x₂ приводит к функции f₂(x₁, x₂, x₂) = x₁+2x₂+7x₂, которая равна функции двух аргументов f₂(x₁, x₂) = x₁+9x₂. Переименование x₁ и x₃ в x₂ приводит к одноместной функции f₃(x₁) = 10x₂.

4) Элементарной функцией в математическом анализе называется всякая функция f, являющаяся суперпозицией фиксированного (т. е. не зависящего от значений аргументов f) числа арифметических функций, а также функций е^x, log х, sin х, arcsin х. Например, функция log²(x₁ + x₂) + 3sin sin x₁ + x₃ элементарна, так как является результатом нескольких последовательных суперпозиций х₁ + x₂, x², log х, Зх, sin х.

5) Всякая непрерывная функция n переменных представима в виде суперпозиции непрерывных функций двух переменных. (Этот результат получен в 1956—1957 гг. в работах А. Н. Колмогорова и В. И. Арнольда и является решением 13-й проблемы Гильберта 14].)

6) Рассмотрим множество {1, 2, 3} и два преобразования этого множества: 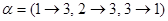и 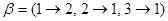. Обычно преобразования конечных множеств записывают так:

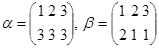
Композиция преобразований — это новое преобразование:

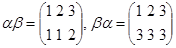
Способы задания функций. Наиболее простой способ задания функций — это таблицы, т. е. конечные списки пар (х, f(х)). Однако таким образом могут быть заданы только функции, определенные на конечных множествах. Таблицы функций, определенных на бесконечных множествах (например, логарифмических, тригонометрических и т. д.), задают эти функции только в конечном числе точек. Для вычисления значений (приближенных!) функций в промежуточных точках служат правила интерполяции.

Другим не менее известным способом задания функций является формула, описывающая функцию как суперпозицию Других (исходных) функций (пример 1-10, п. 4). Если способ вычисления исходных функций известен, то формула задает процедуру вычисления данной функции как некоторую последовательность вычислений исходных функций. Вычисления функций по таблицам, формулам, а также с помощью графиков являются частным видом вычислительных процедур. Для функции, заданной таблицей, процедура заключается в поиске соответствующей строки таблицы; для формулы — в последовательном вычислении всех функций, входящих в суперпозицию. Существуют вычислительные процедуры, не относящиеся к указанным трем видам. Среди них особенно следует выделить рекурсивные процедуры. Рекурсивная процедура задает функцию f, определенную на N, следующим образом: 1) задается значение f(1) (или f(0)); 2) значение f(n+1) определяется через суперпозицию f(n) и других, считающихся известными функций. Простейшим примером рекурсивной процедуры является вычисление функции n!: 1) 0! = 1; 2) (n + 1)! = n!n. В правой части последнего равенства имеется формула, однако это задание функции существенно отличается от задания формулой типа примера 1-10, п. 4. Отличие состоит в том, что для того, чтобы вычислить 8!, необходимо сначала вычислить 7!, тогда как в примере 1-10, п. 4 вычисление для любой тройки аргументов происходит «непосредственно». Более точно для вычисления n! требуется n умножений, т. е. число вычислительных шагов растет с ростом аргумента; для вычисления же функции примера 1-10, п. 4 требуется независимо от значения аргументов всегда одно и то же число шагов (если шагом считать вычисление функции, входящей в суперпозицию), равное восьми.

Наконец, возможны описания функций, которые не содержат способа вычисления функции, хотя сомнений в том, что фикция однозначно задана, не возникает. Определим, например, функцию следующим образом:

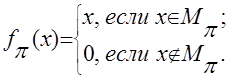
Из описания 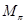(см. §1) не видно, как убедиться в том, что 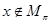, поэтому нет гарантии, что 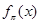можно вычислить.

Отступление 1-3. Для функций возникает тот же вопрос, что и для множеств; что значит «задать функцию»? По смыслу нашего определения задать функцию f: А®В — это значит описать определяющее ее подмножество А ´ В, поэтому вопрос сводится к заданию некоторого множества. Однако можно определить понятие функции, не используя языка теории множеств: функция считается заданной, если задана вычислительная процедура, которая по любому заданному значению аргумента выдает соответствующее значение функции. Функция, определенная таким образом, называется вычислимой. Процедура должна быть эффективной, т. е. однозначно приводящей к результату. Как уже говорилось ранее (см, отступление 1-2), уточнение понятия эффективной процедуры привело к созданию теории алгоритмов.

Понятие эффективной вычислительной процедуры — алгоритма может быть принято за исходное при построении всей системы понятий математики. Такой подход к обоснованию математики, называемый конструктивным, попускает только те математические объекты и утверждения, которые могут быть получены с помощью алгоритмов. С этой точки зрения описанная ранее функция/я вообще не заслуживает названия функции, поскольку для нее не указан алгоритм вычисления. Понятие множества перестает быть первичным; оно определяется с помощью разрешающей или порождающей процедуры (см. § 1-1). Множества, для которых нет таких процедур, просто не рассматриваются.

Достоинства конструктивного подхода достаточно ясны. Однако его последовательное проведение показало, что он требует более радикальной ревизии основных понятий математики, чем это кажется с первого взгляда, и иногда приводит к значительным концептуальным и языковым неудобствам. Поэтому в качестве «математического мировоззрения» конструктивизм разделяется относительно небольшим числом математиков, хотя, пожалуй, никто не отрицает преимуществ конструктивных методов в тех случаях, когда они возможны.

⇐ Предыдущая 1 2 34