Пример 1-9.

Пример 1-9.

1) Функция sin х имеет тип R®R. Отрезок 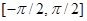она взаимно-однозначно отображает на отрезок [-1, 1]. Поэтому на отрезке [-1, 1] для нее существует обратная функция arcsin х.

2) Ранее приводились примеры кодирующих функций, которые каждому объекту из своей области значений ставят в соответствие некоторый код. Для кодирующей функции обратной будет декодирующая функция, которая каждому коду ставит в соответствие закодированный этим кодом объект. Если кодирующая функция не сюръективна, то декодирующая функция не всюду определена.

Пусть даны функции f: А®В и g: B®C. Функция h: А®C называется композицией функций f и g (обозначение 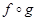), если имеет место равенство h(x)=g(f(x)), где хÎА. Композиция f и g представляет собой последовательное применение функций f и g, g применяется к результату f. Часто говорят, что функция h получена подстановкой f в g. Знак 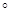аналогично умножению часто опускается.

Для многоместных функций f: А^m®В, g: Bⁿ®C возможны различные варианты подстановки f в g, дающие функции различных типов. Например, при т = 3, n = 4 функция h₁ = g(x₁, f(y₁, y₂, y₃), x₃, x₄) имеет шесть аргументов и тип B´A³´B²®C, а функция h₂= g(f(y₁, y₂, y₃), f(z₁, z₂, z₃), x₃, x₄) имеет восемь аргументов и тип A⁶´B²®C. Особый интерес представляет случай, когда задано множество функций типа . В этом случае возможны, во-первых, любые подстановки функций друг в друга, а во-вторых, любые переименования аргументов, например переименование x₃ в x₂, порождающее из функции f(x₁, x₂, x₃, x₄)функцию трех аргументов f(x₁, x₂, x₂, x₄). Функция, полученная из f₁, ..., f_n некоторой подстановкой их друг в друга и переименованием аргументов, называется суперпозицией f₁, ..., f_n. Выражение, описывающее эту суперпозицию и содержащее функциональные знаки и символы аргументов, называется формулой.

⇐ Предыдущая 1 234 Следующая ⇒