СООТВЕТСТВИЯ И ФУНКЦИИ. Пример 1-7.

СООТВЕТСТВИЯ И ФУНКЦИИ

Соответствия. Соответствием между множествами А и В называется подмножество GÍA´B.

Если (а, b) Î G, то говорят, что b соответствует а при соответствии G. Множество пр₁G называется областью определения соответствия, множество пр₂G — областью значений соответствия. Если пр₁G = А, то соответствие называется всюду определенным (в противном случае соответствие называется частичным); если пр₂G = В, то соответствие называется сюръективным.

Множество всех b Î В, соответствующих элементу а Î А, называется образом а в В при соответствии G. Множество всех а, которым соответствует b, называется прообразом b в А при соответствии G. Если C Î пр₁G, то образом множества С называется объединение образов всех элементов С. Аналогично определяется прообраз множества D для любого D Î пр₂G.

Соответствие G называется функциональным (или однозначным), если образом любого элемента из пр₁G является единственный элемент из пр₂G. Соответствие G между А и В называется взаимно-однозначным (иногда пишут «1-1-соот-ветствие»), если оно всюду определено, сюръективно, функционально и, кроме того, прообразом любого элемента из пр₁G является единственный элемент из пр₂G.

Пример 1-7.

1) Круг G радиуса 1 с центром в точке (3, 2) (рис. 1-1), т. е. множество пар действительных чисел (х, у), удовлетворяющих ' соотношению (х - 3)²+ (у - 2)²£ 1, задает соответствие между R и R (осью абсцисс и осью ординат). Образом числа 4 при этом соответствии является единственное число 2, образом числа 3 является отрезок [1, 3] оси ординат; этот же отрезок [1, 3] является образом отрезка [2, 4] оси абсцисс, который, в свою очередь, служит прообразом числа 2. Данное соответствие не является функциональным. Примером функционального соответствия между действительными числами на том же рис.1-1служит дуга АВС.

Еще раз напомним, что для задания соответствия надо указать не только множество G, но и множества А и В, т. е. указать, подмножеством какого именно прямого произведения является G. В данном примере тот же круг G₁ задает и другое соответствие: между отрезком [2, 4] и отрезком [1, 3]. При этом по некоторым свойствам соответствия G₁ Í R² и G₁ Í [2, 4] ´ [1, 3] отличаются: например, второе соответствие в отличие от первого всюду определено и сюръективно. Учитывая эти соотношения, следовало бы определять соответствие как тройку множеств (G, А, В), как это сделано в [6]. Тогда не пришлось бы оговариваться, что один круг может задавать два соответствия; это и так было бы ясно из различия троек (G₁, R, R) и (G₁, [2,4],[1, 3]). Однако такие оговорки приходится делать редко: либо множества А и В ясны из контекста, либо различия в их выборе не влияют на исследуемые свойства соответствия. Поэтому «определение через тройку множеств» здесь использоваться не будет.

2) Англо-русский словарь устанавливает соответствие между множеством английских и русских слов. Это соответствие не является функциональным (так как одному английскому слову, как правило, ставится в соответствие несколько русских слов); кроме того, оно практически никогда не является полностью определенным: всегда можно найти английское слово, не содержащееся в данном словаре.

3) Позиция на шахматной доске представляет собой взаимно-однозначное соответствие между множеством оставшихся на доске фигур и множеством занятых ими полей.

4) Различные виды кодирования — кодирование букв азбукой Морзе, представления чисел в различных системах счисления, секретные шифры, входящие и исходящие номера в деловой переписке и другие — являются соответствиями между кодируемыми объектами и присваиваемыми им кодами. Эти соответствия, как правило, обладают всеми свойствами взаимно-однозначного соответствия, кроме, быть может, одного — сюръективности, Единственность образа и прообраза в кодировании гарантирует однозначность шифровки и дешифровки. Отсутствие сюръективности означает, что не всякий код имеет смысл, т.е. соответствует какому-либо объекту. Например, кодирование телефонов г. Москвы семизначными номерами не сюръективно, так как некоторые семизначные номера не соответствуют никаким телефонам.

5) Множество векторов вида (n, 2ⁿ), где n Î N, задает взаимно-однозначное соответствие между множеством N натуральных чисел и множеством М₂ⁿ степеней двойки.

Взаимно-однозначные соответствия и мощности множеств. Если между конечными множествами А и В существует взаимно-однозначное соответствие, то 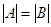. Действительно, если это не так, то либо 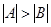и тогда, поскольку отображение всюду определено, в А найдутся два элемента, которым соответствует один и тот же элемент bÎB (нарушится единственность образа), либо 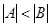и тогда, поскольку отображение сюръективно, в В найдутся два элемента, соответствующих одному и тому же a Î B (нарушится единственность прообраза). ^ Обращаем внимание на то, что в этом простом рассуждении оказываются существенными все четыре свойства взаимно-однозначного соответствия.

Этот факт, во-первых, позволяет установить равенство мощностей двух множеств, не вычисляя этих мощностей, а во-вторых, часто дает возможность вычислить мощность множества, установив его взаимно-однозначное соответствие с множеством, мощность которого известна или легко вычисляется. В качестве иллюстрации этого приема докажем важную теорему о числе подмножеств конечного множества.

Теорема 1-2. Если для конечного множества A 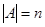то число всех подмножеств А равно 2ⁿ, т.е. .

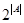Занумеруем элементы А номерами от 1 до n: A = { a₁, a₂, …, a_n } и рассмотрим множество В_n двоичных векторов из нулей и единиц длины n. Каждому подмножеству А^*Î А поставим в соответствие вектор v=(v₁, v₂, …, v_n) Î В_n следующим образом:

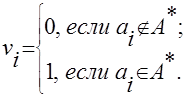
Например, если А = {а, Ь, с, d, е}, то подмножеству {а, с, d} соответствует вектор (1, 0, 1, 1, 0), а подмножеству {Ь} соответствует вектор (0, 1, 0, 0, 0). Пустому подмножеству любого А соответствует вектор из одних нулей, а самому А — вектор из одних единиц. Очевидно, что установленное соответствие между множеством всех подмножеств А и двоичными векторами длины n является взаимно-однозначным и число подмножеств А равно 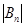. А так как В_n является прямым произведением n двухэлементных множеств {0, 1}, то в силу следствия из теоремы 1-1 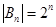.ð

Множества равномощны, если между их элементами можно установить взаимно-однозначное соответствие. Для конечных множеств это утверждение доказывается, что и было сделано ранее. Для бесконечных множеств оно является определением равномощности. Множества, равномощные N, называются счетными. Соответствие, установленное в примере 1-7, п. 5, показывает, что множество М₂ⁿ счетно. Вообще любое бесконечное подмножество N счетно. Действительно, пусть N` Ì N. Выберем в N` наименьший элемент и обозначим его n₁, в N` \{n₁} выберем наименьший элемент и обозначим его n₂; наименьший элемент N` \{n₁, n₂} обозначим n₂ и т. д. Поскольку для всякого натурального числа имеется лишь конечное множество меньших натуральных чисел, то любой элемент N` рано или поздно получит свой номер. Эта нумерация, т. е. Соответствие (n_i, i), и есть взаимно-однозначное соответствие между N` и N.

Множество N² .счетно. Нумерацию N² можно устроить следующим образом. Разобьем N² на классы. К первому классу 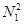отнесем все пары чисел с минимальной суммой. Такая пара всего одна: (1, 1). Ко второму классу 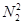отнесем все пары чисел с суммой 3: 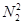= {(1, 2), (2, 1)}. В общем случае 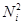= {(a, b) | a + b = i + 1}. Каждый класс 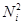содержит ровно i пар. Упорядочим теперь классы по возрастанию индексов i, а пары внутри класса — по возрастанию первого элемента и занумеруем получившуюся последовательность пар номерами 1, 2, 3 ... Легко видеть, что если а + b = i + 1, то пара (а, b) получит номер 1 + 2 + ... + (i—1) +а. Эта нумерация и доказывает счетность N², из которой, в свою очередь, непосредственно следует счетность множества Р положительных рациональных чисел, т.е. дробей вида a/b, где a и b — натуральные числа. Аналогично доказывается счетность N³ и вообще N^kдля любого натурального k.

Нетрудно понять, что объединение конечного числа счетных множеств M₁, M₂, ..., M_k счетно. Действительно, перенумеруем сначала все первые элементы множеств, затем все вторые и т. д. Объединение счетного множества конечных множеств также счетно (сначала нумеруем все элементы первого множества, затем все элементы второго множества и т. д.). Из последнего утверждения следует, что множество всех слов в любом конечном алфавите счетно. Менее очевидно, что счетно и объединение счетного множества счетных множеств. Примером такого объединения является множество 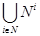всех векторов с натуральными компонентами.

Множество всех действительных чисел отрезка [0, 1] не является счетным (теорема Кантора). Действительно, предположим, что оно счетно и существует его нумерация. Расположим все числа, изображенные бесконечными десятичными дробями, в порядке этой нумерации:

0,	a₁₁,	a₁₂,	a₁₃,	…
0,	a₂₁,	a₂₂,	a₂₃,	…
0,	a₃₁,	a₃₂,	a₃₃,	…
…	…	…	…	…

Рассмотрим любую бесконечную десятичную дробь 0, b₁, b₂, b₃, ..., такую, что b₁¹a₁₁, b₂¹a₂₂, b₃¹a₃₃ и т.д. Эта дробь не может войти в указанную последовательность, так как от первого числа она отличается первой цифрой, от второго числа — второй цифрой и т. д. Следовательно, все числа из отрезка [0, 1] не могут быть пронумерованы и множество всех действительных чисел отрезка [0, 1] несчетно. Его мощность называется континуум', множества такой мощности называются континуальными. Метод, использованный при доказательстве, называется диагональным методом Кантора.

Множество всех подмножеств счетного множества континуально. Это становится ясным, если воспользоваться, как и в теореме 1-2, представлением подмножества в виде последовательности (но теперь уже бесконечной!) нулей и единиц: на i-ом месте стоит 1, если i-й элемент множества входит в данное подмножество, и 0 в противном случае. Получаем взаимно-однозначное соответствие между подмножествами счетного множества и правильными двоичными дробями, которые в свою очередь, взаимно-однозначно соответствуют множеству чисел отрезка [0, 1]. Как показывается в теории множеств (с помощью метода, аналогичного диагональному), для множества любой мощности множество его подмножеств имеет более высокую мощность. Поэтому не существует множества максимальной мощности. Парадокс, приведенный в отступлении 1-2 (парадокс Кантора), как раз и заключается в том, что «множество всех множеств» должно содержать все множества и, следовательно иметь максимальную мощность, что противоречит результатам теории множеств.

Отображения и функции. Функцией называется функциональное соответствие. Если функция f устанавливает соответствие между множествами A и B, то говорят, что функция f имеет тип А®В (обозначение f: А®В). Каждому элементу а из своей области определения функция f ставит в соответствие единственный элемент b из области значений. Это обозначается хорошо известной записью f(а)=b. Иногда, если это не вызывает неудобств, используют обозначения fa или af. Элемент а называется аргументом функции, b — значением функции на а. Полностью определенная функция f: А®В называется отображением А в В. Образ А при отображении f обозначается f(А). Если соответствие f при этом сюръективно, т. е. каждый элемент В имеет прообраз в А, то говорят, что имеет место отображение А на В (сюръективное отображение). Если f(А) состоит из единственного элемента, то f называется функцией-константой. Отображение типа А®А часто называют преобразованием множества А.

Функции f и g равны, если их область определения — одно и то же множество А и для любого аÎА f(а) = g(а).

12 3 4 Следующая ⇒