Хелпикс

Главная

Контакты

Случайная статья



ый случай.. ый случай.

⇐ ПредыдущаяСтр 3 из 4Следующая ⇒


4-ый случай.

                             

                                                                    

 

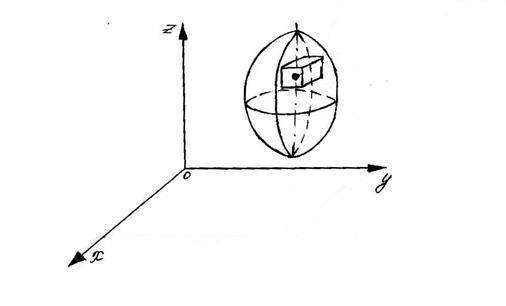
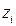
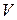
Пусть в ограниченной замкнутой и кубируемой (имеет объем) области 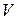 пространства, задана 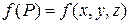- непрерывная скалярная функция точки, т.е. функция, принимающая в каждой точке  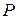из области  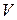определенные значения.

Выполним следующие операции:

1) Область 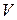 разобьем произвольным образом на n – кубируемых частей. Занумеруем их и обозначим 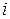-ую часть и ее площадь через 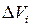; 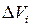-элемент разбиения. .

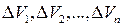2) В каждой получившейся при этом части 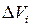 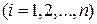выберем произвольно точку 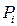,  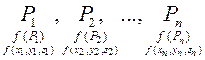и вычислим .

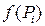3) Каждое значение 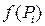умножим на объем  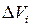соответствующей части, т.е. составим произведения вида:

 

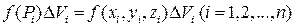
4) Составим сумму всех этих произведений:

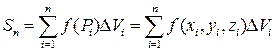
      Эту сумму будем называть трехмерной или тройной   интегральной                    суммой.

5) Найдем предел суммы 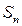 при стремлении к нулю наибольшего

    из диаметров частей разбиения (при этом число частей разбиения будет неограниченно возрастать при ).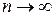

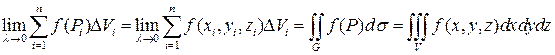
Это тройной интеграл от функции 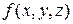 по области 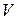.  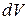- элемент объема.

 

 

5-ый случай.

                                                         

 

 

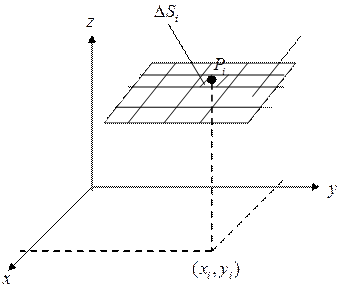
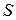
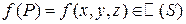- непрерывная в каждой точке поверхности S  функция.

1) Поверхность S разобьем произвольным образом на n частей. Занумеруем их и обозначим 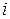-ую часть и ее площадь через 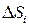; 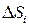-это площадь элемента деления, .

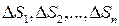2) В каждой получившейся при этом части 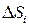 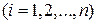выберем произвольно точку 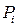,  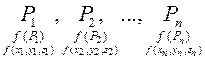и вычислим .

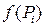3) Каждое значение 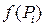умножим на взятую площадь  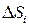соответствующей части, т.е. составим произведения вида:

 

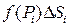
4) Составим сумму всех этих произведений:

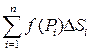
      Эту сумму будем называть интегральной по поверхности S.

 

4) Найдем предел суммы:

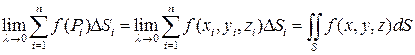
Это есть поверхностный интеграл I-го рода.

 

§11.2 ОПРЕДЕЛЕНИЕ ПЛОТНОСТИ ДЛЯ РАССМАТРИВАЕМЫХ МАТЕРИАЛЬНЫХ ФИГУР.


⇐ Предыдущая1234Следующая ⇒
  

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.