
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
ГЛАВА 11. КРАТНЫЕ, КРИВОЛИНЕЙНЫЕ И ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ.
ГЛАВА 11. КРАТНЫЕ, КРИВОЛИНЕЙНЫЕ И ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ.
§11.1 ОПРЕДЕЛЕНИЕ , КРИВОЛИНЕЙНЫХ, ДВОЙНЫХ, ТРОЙНЫХ И ПОВЕРХНОСТНЫХ ИНТЕГРАЛОВ.
Df.1 Назовем фигурой либо линию в пространстве, или на плоскости, в частности это может быть отрезок оси, либо плоскую область, либо некоторое пространственное тело, либо поверхность в пространстве.
 1)
1) 
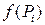 ●
● 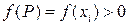 2)
2) 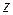
 ●
● 
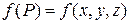
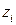

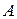 ●
● 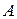 ●
● 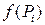
0 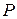 ● 0
● 0 
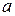
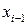
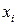
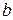 ●
●
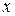

3) 
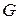

● 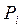
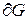

 ●
● 

● 
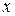
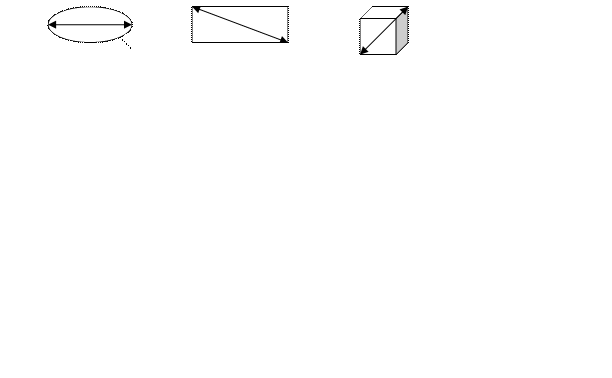
Df.2 Назовем диаметром фигуры максимальное из расстояний между двумя точками этой фигуры. Т.е.  .
. 
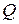
и т.д.
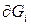
Df.3 Рассматривая фигуры различных типов будем говорить о их мере. Т.е. термин «мера» - мера множества A:

Если 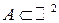 , то
, то 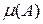 - площадь множества A;
- площадь множества A;  , то
, то 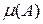 - объем множества A.
- объем множества A.
Аналогично понятие меры обобщается на 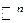 .
.
В случае линий под мерой будет пониматься их длина, а случае пространственных тел – площадь.
Пусть на каждой фигуре G задана скалярная функция f(P)/
Для каждой фигуры совершим одни и теже действия.
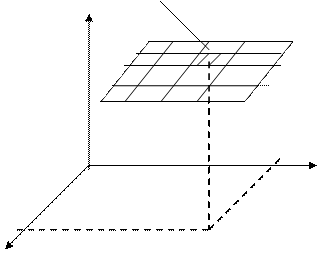
1. Разобьем каждую фигуру произвольным образом на n- частей.
2. На каждой части возьмем точку  и определим значение функции в этой точке
и определим значение функции в этой точке 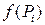 .
.
3. Значение 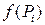 умножим на меру соответствующей части.
умножим на меру соответствующей части.
4. Все полученные произведения суммируем (т.е. сложим).
Df.4 Полученная в результате перечисленных операций сумма, носит
название «n-ой» интегральной суммы.
Пусть 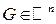 , G – измеримое множество.
, G – измеримое множество. 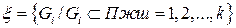 -совокупность подмножеств множества G, что:
-совокупность подмножеств множества G, что:
а) 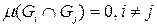 .
.
б) 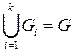 .
.
Тогда 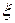 есть разбиение G. Так например:
есть разбиение G. Так например:
n=2.

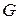

0 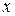
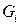
Используя обозначение  :
:


 Df.5 Шагом (мелкостью) разбиения
Df.5 Шагом (мелкостью) разбиения 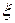 называется
называется 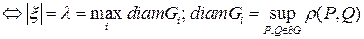 , где
, где 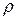 - это расстояние ,
- это расстояние , 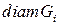 - длина максимальной хорды.
- длина максимальной хорды. 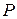
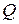

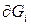
Пунктированным разбиением множества  совокупность разбиения
совокупность разбиения 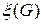 и набора точек
и набора точек 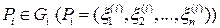 , обозначение
, обозначение 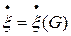 .
.
Очевидно, данному разбиению 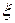 может соответствовать бесконечно много пунктированных разбиений
может соответствовать бесконечно много пунктированных разбиений 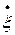 в зависимости от расположения точек
в зависимости от расположения точек 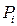 . Шаг пунктированного разбиения:
. Шаг пунктированного разбиения:
 .
.
Пусть на 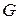 определена скалярная функция
определена скалярная функция 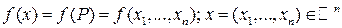 , фиксируем некоторое пунктирное разбиение
, фиксируем некоторое пунктирное разбиение  . Сумма вида:
. Сумма вида:
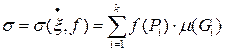 (1)
(1)
называется интегральной суммой Римана или просто интегральной суммой.
Кратным интегралом (интегралом Римана) от функции  ,
, 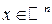 по множеству
по множеству 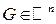 называется:
называется:
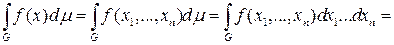
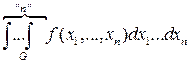 =
=
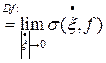 ,
,
если последний предел существует и конечен.
При n=2 (двойной интеграл), 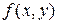 :
:
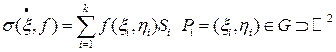 ,
, 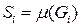 - площадь
- площадь  .
.
Обозначение:

При n=3 (тройной интеграл), 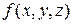 :
:
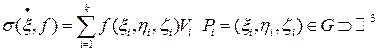 .
.
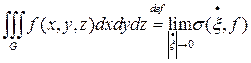 .
.
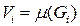 - объем
- объем  .
.
Отметим, что при n=1 это определение отлично от данного ранее. Здесь 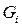 любое измеримое множество, а не отрезок, как в определенном интеграле. Однако можно показать их эквивалентность.
любое измеримое множество, а не отрезок, как в определенном интеграле. Однако можно показать их эквивалентность.
Df.6 Если  определена на
определена на 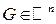 и
и 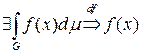 интегрируема на
интегрируема на 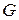 по Риману.
по Риману.  - множество функций, интегрируемых по Риману на
- множество функций, интегрируемых по Риману на 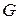 .
.
Для всех рассматриваемых фигур, пользуясь предложенной схемой, составим интегральные суммы.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|