Фронтальная работа.

Вывод уравнения колебаний струны. Формулировка краевой задачи. Вывод уравнений электрических колебаний в проводах

В математической физике под струной понимают гибкую, упругую нить. Напряжения, возникающие в струне в любой момент времени, направлены по касательной к ее профилю. Пусть струна длины 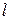в начальный момент направлена по отрезку оси от О до 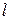. Предположим, что концы струны закреплены в точках х = 0 и х = 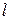. Если струну отклонить от ее первоначального положения, потом предоставить самой или, не отклоняя струны, придать в начальный момент ее точкам некоторую скорость, то точки струны будут совершать движение – говорят, что струна начнет колебаться. Задача заключается в определении формы струны в любой момент времени в зависимости от времени.

Будем рассматривать малые отклонения точек струны от начального положения. В силу этого можно предполагать, что движение точек струны происходит перпендикулярно оси Ох и в одной плоскости. При этом предположении процесс колебания струны описывается одной функцией и(х,t), которая дает величину перемещения точки струны с абсциссой х в момент t.

Так как рассматриваем малые отклонения струны в плоскости (х,u), то будем предполагать, что длина элемента струны 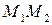равняется ее проекции на ось Ох, т.е. Также будем предполагать, что натяжение во всех точках струны одинаковое; обозначим его через Т.

Рассмотрим элемент струны (рис. 390). На концах этого элемента, по касательным к струне, действуют силы Т. Пусть касательные образуют с осью Ох углы 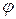и 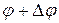Тогда проекция на ось Ои сил, действующих на элемент ММ', будет равна Т sin ( 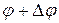) – Т sin 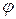. Так как угол 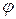мал, то можно положить tg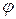 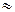sin 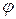, и мы будем иметь

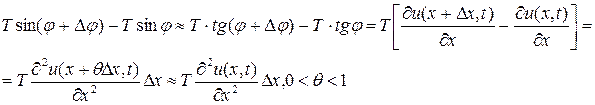
(здесь мы применили теорему Лагранжа к выражению, стоящему в квадратных скобках).

Чтобы получить уравнение движения, нужно внешние силы, приложенные к элементу, приравнять силе инерции. Пусть р — линейная плотность струны. Тогда масса элемента струны будет 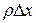. Ускорение элемента равно 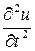. Следовательно, по принципу Даламбера будем иметь:

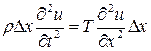Сокращая на Δх и обозначая 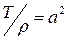, получаем уравнение движения . (1)

Это и есть волновое уравнение — уравнение колебаний струны. Для полного определения движения струны одного уравнения (1) недостаточно. Искомая функция u(х, t) должна удовлетворять еще граничным условиям, указывающим, что делается на концах струны (х = 0 и х = l), и начальным условиям, описывающим состояние струны в начальный момент (t = 0). Совокупность граничных и начальных условий называется краевыми условиями. Пусть, например, как мы предполагали, концы струны при х = 0 _и х — l неподвижны. Тогда при любом t должны выполняться равенства

u(0,t)=0, (2')

и (l, t) = 0. (2")

эти равенства являются граничными условиями для нашей задачи.

В начальный момент t = 0 струна имеет определенную форму, которую мы ей придали. Пусть эта форма определяется функцией f(x). Таким образом, должно быть

( )

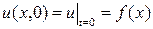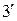Далее, в начальный момент должна быть задана скорость в каждой точке струны, которая определяется функцией 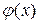. Таким образом, должно быть

. ( )

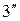Условия (3') и (3") являются начальными условиями.

Замечание. Вчастности, может быть 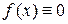или 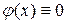. Если же 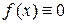и 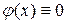, то струна будет находиться в покое, следовательно, .

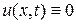Как указывалось выше, к уравнению (1) приводит и задача об электрических колебаниях в проводах. Покажем это. Электрический ток в проводе характеризуется величиной и напряжением v(x, t), которые зависят от координаты х точки провода и от времени t. Рассматривая элемент провода Δx, можем написать, что падение напряжения на элементе Δх равно

v(x, t) – v(x + Δx, t) 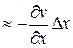. Это падение напряжения складывается

из омического, равного 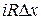, и индуктивного, равного . Итак,

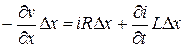, (4)

где R и L — сопротивление и коэффициент индуктивности, рассчитанные на единицу длины провода. Знак минус взят потому, что ток течет в направлении, обратном возрастанию v. Сокращая на Δх, получаем уравнение

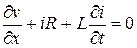
Далее, разность токов, выходящего из элемента Δх и входящего в него за время Δt, будет

Она расходуется на зарядку элемента, равную 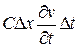, и на утечку через боковую поверхность провода вследствие несовершенства изоляции, равную AvΔxΔt (здесь А — коэффициент утечки) Приравнивая эти выражения и сокращая на Δх; Δt, получим уравнение

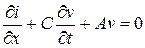. (6)

Уравнения (5) и (6) принято называть телеграфными уравнениями.

Из системы уравнений (5) и (6) можно получить уравнение, содержащее только искомую функцию i(x, t), и уравнение, содержащее только искомую функцию 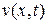. Продифференцируем члены уравнения (6) по х; члены уравнения (5) продифференцируем по t и умножим их на С. Производя вычитание, получим

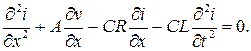
Подставляя в последнее уравнение выражение 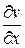из уравнения (5), получим

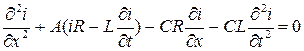
или

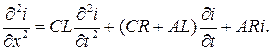(7)

Аналогичным образом получается уравнение для определения

v{x, t):

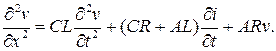(8)

Если можно пренебречь утечкой через изоляцию (А = 0) и сопротивлением

(R = 0), то уравнения (7) и (8) переходят в волновые уравнения

, ,

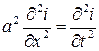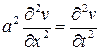где обозначено: 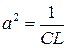. Исходя из физических условий, формулируются граничные и начальные условия задачи.

Фронтальная работа.

⇐ Предыдущая 1 234 Следующая ⇒