Практическое занятие №5.. Краткие теоретические сведения.. Общие сведения.. где незавершенная запись в конце скобок означает, что за могут браться и иные частные производные m-го порядка от и.

Практическое занятие №5.

Тема«Решение простейших дифференциальных уравнений линейных относительно частных производных ».

ЦелиНаучиться решать простейшие дифференциальные уравнения в частных производных и дифференциальные уравнения первого порядка, линейные относительно частных производных.

Краткие теоретические сведения.

Общие сведения.

До сих пор, рассматривая дифференциальные уравнения, мы занимались лишь обыкновенными дифференциальными уравнениями. Однако в ряде вопросов самой математики, а также ее приложений (особенно к физике) встречается необходимость разыскивать функцию от нескольких переменных х_1у х₂, ..., х_п из некоторого уравнения в частных производных. Общий вид уравнения в частных производных таков:

(1) где незавершенная запись в конце скобок означает, что за могут браться и иные частные производные m-го порядка от и.

Порядком m дифференциального уравнения в частных производных называется наивысший из порядков частных производных, входящих в это уравнение.

Всякая функция и = φ(х_1} х₂, ..., х_п), удовлетворяющая уравнению (1), называется его решением. Как и для обыкновенных дифференциальных уравнений, здесь снова возникает вопрос об общем решении и параметрах (произвольных «постоянных»). Вопрос этот, однако, для уравнений в частных производных представляет более сложную проблему, чем для обыкновенных дифференциальных уравнений. Не давая общих определений, сюда относящихся, мы сделаем по этому поводу лишь некоторые замечания.

Если, например, уравнение в частных производных первого порядка для функции и от п переменных х₁, х₂, ,.., х_п включает только одну какую-либо частную производную, например , то, фиксируя значения остальных переменных

х₂, х_а, ..., х_п, мы получим обыкновенное дифференциальное уравнение первого порядка относительно и как функции от х₁,и тогда общее решение такого уравнения будет иметь вид: , где С — произвольное постоянное. Однако здесь для нас существенно лишь то, чтобы частная производная удовлетворяла взятому уравнению в частных производных, а тогда С может быть здесь взято не обязательно абсолютной постоянной, а и какой-либо функцией от х₂, х₃, ..., х_п: С = 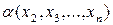, т. е. общее решение уравнения в частных производных первого порядка с одной лишь частной производной по должно содержать одну произвольную функцию от остальных переменных. Так, если для функции и от переменных x и y дано уравнение в частных производных , то общее решение его будет иметь вид:

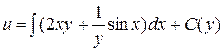, т. е. , где С (у) — произвольная функция от у (определенная для у ≠ 0).

Если, далее, это уравнение с одной частной производной (например, взятой по х_х) будет второго (или вообще n-го) порядка, то очевидно, следует ожидать, что в общем решении будет содержаться две (или вообще п) таких произвольных функций от остальных аргументов х₂, х₃, ..., х_п.

Как и для обыкновенных дифференциальных уравнений, для уравнений m-го порядка в частных производных, разрешенных относительно одной из своих частных производных 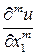, т. е. для уравнения вида 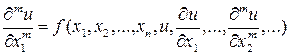, (2)

рассматривается вопрос о частном решении, удовлетворяющем некоторым специальным условиям (которые однозначно определяют это решение для (2), хотя бы из некоторого класса функций).

Существуют теоремы, которые доказывают при тех или иных ограничениях существование и единственность такого решения.

В вопросах математической физики часто встречаются уравнения в частных производных второго порядка и, прежде всего, однородные относительно этих производных уравнения. Для случая функции и (х, у) двух переменных такое уравнение имеет вид:

. (3)

Запись коэффициентов здесь произведена по аналогии с тем, как записывают уравнение кривой второго порядка в аналитической геометрии, и аналогия эта дает основания для классификации уравнений вида (3) по дискриминанту: , по которому они подразделяются на уравнения эллиптического ( 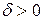), гиперболического ( 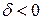) и параболического ( 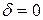) типа.

Функция и(х, у), являющаяся решением дифференциального уравнения (3), часто задается в виде суммы некоторого ряда 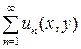, члены которого есть функции от двух переменных. Такой ряд называется сходящимся в точке (х₀, у₀), если соответствующий числовой ряд 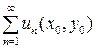сходится. Точно так же, как и для обычных рядов, здесь устанавливается понятие области сходимости ряда, выводятся правила почленного дифференцирования и интегрирования таких рядов (по какому-либо из переменных) и т. д.

Основные типы уравнений математической физики

Основными уравнениями математической физики называют (для случая функций двух независимых переменных) следующие дифференциальные уравнения с частными производными второго порядка.

I. Волновое уравнение:

12 3 4 Следующая ⇒