Задание 14 № 514245. Решение.. Задание 15 № 511529. Решение.. Задание 16 № 509123. Решение.. Задание 17 № 517753. Решение.. Задание 18 № 504833. Решение.. Замечание.

14. Задание 14 № 514245

В правильной четырёхугольной пирамиде SABCD все рёбра равны 5. На рёбрах SA, AB, BC взяты точки P, Q, R соответственно так, что PA = AQ = RC = 2.

а) Докажите, что плоскость PQR перпендикулярна ребру SD.

б) Найдите расстояние от вершины D до плоскости PQR.

Решение.

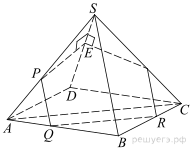а) Стороны треугольника SBD равны 5, 5 и 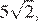поэтому он прямоугольный, то есть прямая SD перпендикулярна прямой SB. Очевидно, что прямые SB и PQ параллельны как стороны равносторонних треугольников, тогда прямая SD перпендикулярна прямой PQ. Прямая AC перпендикулярна прямой BD, и по теореме о трёх перпендикулярах прямая AC перпендикулярна прямой SD, а значит, и прямая QR перпендикулярна прямой SD. Таким образом, плоскость PQR перпендикулярна ребру SD.

б) Пусть плоскость PQR пересекает ребро SD в точке E. Из доказанного следует, что прямая PE перпендикулярна прямой SD, откуда

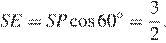
Значит, 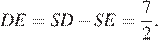Поскольку плоскость PQR перпендикулярна ребру SD, искомое расстояние равно DE.

Ответ: б)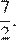

15. Задание 15 № 511529

Решите неравенство: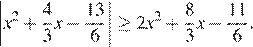

Решение.

Неравенство равносильно совокупности:

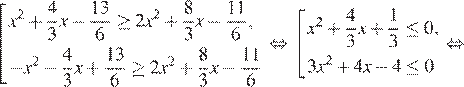
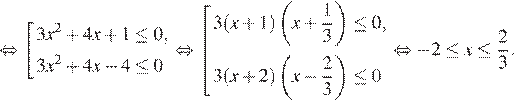
Ответ: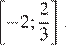

16. Задание 16 № 509123

Точка О — центр окружности, описанной около остроугольного треугольника ABC. На продолжении отрезка AO за точку О отмечена точка K так, что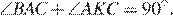

а) Докажите, что четырехугольник OBKC вписанный.

б) Найдите радиус окружности, описанной около треугольника KBC, если известно, что радиус окружности, описанной около треугольника АBC равен 12, а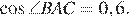

Решение.

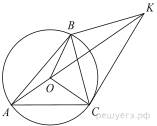а) Пусть тогда 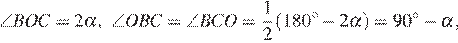как углы при основании равнобедренного треугольника OBC. Из условия 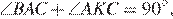следует, что 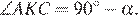Тогда Откуда, по свойству вписанных углов, следует, что точки О, В, К, С лежат на одной окружности.

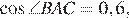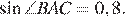б) По условию, тогда Рассмотри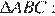м в нем 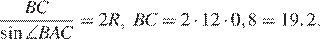В обозначениях пункта 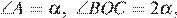а): тогда 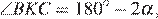так как четырехугольник OBKC вписанный.

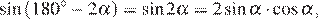
тогда

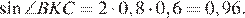
Рассмотрим треугольник KBC:

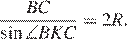
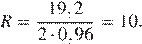
Ответ:10.

17. Задание 17 № 517753

Вадим является владельцем двух заводов в разных городах. На заводах производятся абсолютно одинаковые товары при использовании одинаковых технологий. Если рабочие на одном из заводов трудятся суммарно 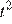часов в неделю, то за эту неделю они производят t единиц товара.

За каждый час работы на заводе, расположенном в первом городе, Вадим платит рабочему 500 рублей, а на заводе, расположенном во втором городе, — 300 рублей.

Вадим готов выделять 1 200 000 рублей в неделю на оплату труда рабочих. Какое наибольшее количество единиц товара можно произвести за неделю на этих двух заводах?

Решение.

Допустим, что на заводе, расположенном в первом городе, рабочие трудятся 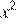часов, а на заводе, расположенном во втором городе, 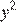часов. Тогда в неделю будет произведено 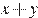единиц товара, а затраты на оплату труда составят 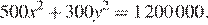Выразим y через x:

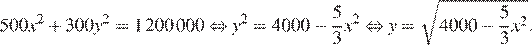
Значит, нам нужно найти наибольшее значение функци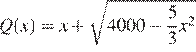и при 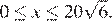Для этого найдем производную функции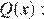

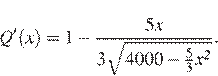
Найдем критические точки:

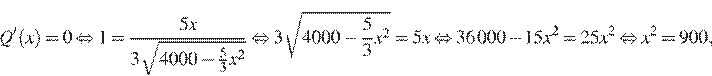
то есть 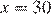— единственная критическая точка, удовлетворяющая условию 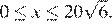Найдем значения функции в найденной точке и на концах отрезка:

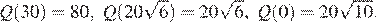
Наибольшее значение функции 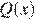равно 80, значит, наибольшее количество единиц товара равно 80.

Ответ: 80.

18. Задание 18 № 504833

Найдите все значения 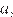при которых неравенство 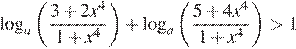выполняется для всех действительных значений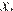

Решение.

Заметим, что

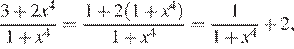
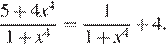
Пусть 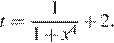Ввиду того, что 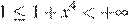множеством значений выражения 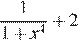при 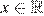является промежуток 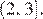Значит, неравенство 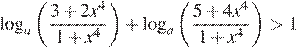выполняется для всех действительных значений 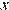тогда и только тогда, когда на промежутке 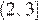выполняется неравенство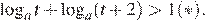

Далее имеем:

1) если 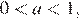то неравенство 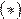не имеет решений на промежутке 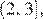так как на этом промежутке оба слагаемых левой части неравенства отрицательны;

2) если 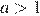, то неравенство 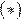равносильно неравенству

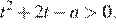
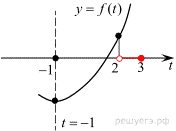
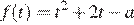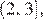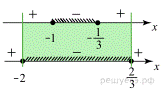
Функция должна быть положительна на промежутке значит, ее график должен быть расположен выше интервала 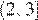оси абсцисс, то есть, должно выполняться условие 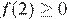(см.рисунок). Решая неравенство 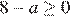с учетом условия 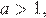окончательно получаем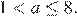

Ответ: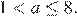

Замечание.

Пункт 2) можно выполнить иначе с помощью следующих рассуждений:

Поскольку вершина параболы 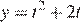имеет координаты 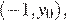функция 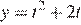возрастает на промежутке 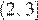и, значит, множеством ее значений на этом промежутке является промежуток 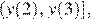то есть промежуток 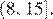Таким образом, неравенство 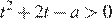верно для всех 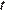из промежутка 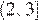в том и только в том случае, когда выполняется условие 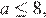откуда с учетом условия 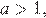окончательно получаем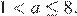

19. Задание 19 № 505539

Все члены конечной последовательности являются натуральными числами. Каждый член этой последовательности, начиная со второго, либо в 10 раз больше, либо в 10 раз меньше предыдущего. Сумма всех членов последовательности равна 3024.

а) Может ли последовательность состоять из двух членов?

б) Может ли последовательность состоять из трёх членов?

в) Какое наибольшее количество членов может быть в последовательности?

Решение.

а) Если последовательность состоит из двух членов, 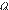и 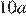(в произвольном порядке), то 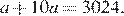Уравнение 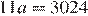не имеет решений в натуральных числах. Поэтому последовательность не может состоять из двух членов.

б) Последовательность может состоять из трёх членов: 252, 2520, 252.

в) Приведём пример последовательности из 549 членов: 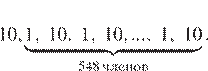Сумма её членов равна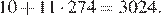

Допустим, что в последовательности более чем 549 членов. Разобьём первые 550 членов последовательности на 275 пар соседних членов: первый и второй, третий и четвёртый, пятый и шестой и т. д. Сумма двух членов в каждой паре делится на 11 и поэтому не меньше 11. Значит, сумма всех членов последовательности не меньше, чем 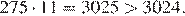Получили противоречие.

Ответ: а) нет, б) да, в) 549.

Ключ

№ п/п

№ задания

Ответ

0,65

6,4

1,62

-2

а) 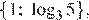б)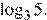

б)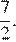

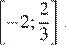
10.

80.

а) нет, б) да, в) 549.

⇐ Предыдущая 1 2 34