
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Задание 9 № 64769. Решение.. Задание 10 № 505403. Решение.. Задание 11 № 516296. Решение.. Задание 12 № 129961. Решение.. Задание 13 № 513605. Решение.. Примечание.
9. Задание 9 № 64769
Найдите 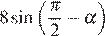 , если
, если 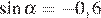 и
и 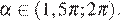
Решение.
Выполним преобразования:
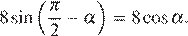
Угол 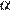 лежит в четвертой четверти, поэтому
лежит в четвертой четверти, поэтому 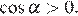 Тогда
Тогда
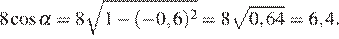
Ответ: 6,4.
10. Задание 10 № 505403
Расстояние от наблюдателя, находящегося на небольшой высоте  километров над землёй, до наблюдаемой им линии горизонта вычисляется по формуле
километров над землёй, до наблюдаемой им линии горизонта вычисляется по формуле 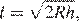 где
где 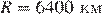 — радиус Земли. С какой высоты горизонт виден на расстоянии 144 километров? Ответ выразите в километрах.
— радиус Земли. С какой высоты горизонт виден на расстоянии 144 километров? Ответ выразите в километрах.
Решение.
Задача сводится к решению уравнения 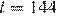 при заданном значении R:
при заданном значении R:
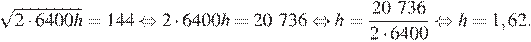
Ответ: 1,62.
11. Задание 11 № 516296
От пристани 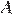 к пристани
к пристани 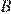 , расстояние между которыми равно 154 км, отправился с постоянной скоростью первый теплоход, а через 3 часа после этого следом за ним со скоростью на 3 км/ч большей, отправился второй. Найдите скорость первого теплохода, если в пункт
, расстояние между которыми равно 154 км, отправился с постоянной скоростью первый теплоход, а через 3 часа после этого следом за ним со скоростью на 3 км/ч большей, отправился второй. Найдите скорость первого теплохода, если в пункт 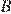 оба теплохода прибыли одновременно. Ответ дайте в км/ч.
оба теплохода прибыли одновременно. Ответ дайте в км/ч.
Решение.
Пусть 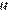 км/ч — скорость первого теплохода, тогда скорость второго теплохода по течению равна
км/ч — скорость первого теплохода, тогда скорость второго теплохода по течению равна 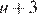 км/ч. Первый теплоход находился в пути на 3 часа больше, чем второй, отсюда имеем:
км/ч. Первый теплоход находился в пути на 3 часа больше, чем второй, отсюда имеем:
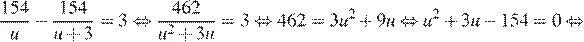
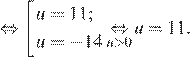
Таким образом, скорость первого теплохода равна 11 км/ч.
Ответ: 11.
12. Задание 12 № 129961
Найдите наибольшее значение функции 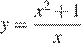 на отрезке
на отрезке 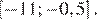
Решение.
Найдем производную заданной функции:
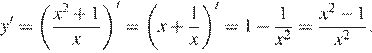
Производная обращается в нуль в точках 1 и −1, заданному отрезку принадлежит только число −1. Определим знаки производной функции и изобразим на рисунке поведение функции на заданном отрезке:
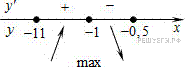
Наибольшим значением функции на заданном отрезке будет 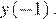 Найдем его:
Найдем его:
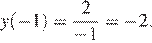
Ответ: −2.
13. Задание 13 № 513605
а) Решите уравнение 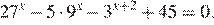
б) Укажите корни этого уравнения, принадлежащие отрезку 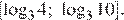
Решение.
а) Разложим левую часть на множители:
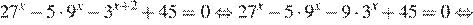
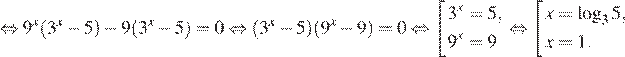
б) Поскольку 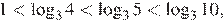 отрезку
отрезку 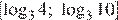 принадлежит только корень
принадлежит только корень 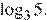
Ответ: а) 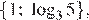 б)
б) 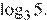
Примечание.
Можно было ввести замену 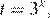 получить уравнение и решить его разложением на множители:
получить уравнение и решить его разложением на множители:
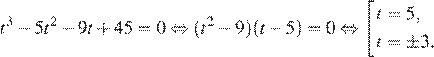
Возвращаясь к исходной переменной получаем решение.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|