Учет краевых условий исходной постановки.

2.6. Учет краевых условий исходной постановки.

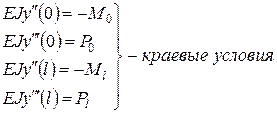(31)

Как следует из формулы (5) поперечные силы 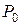и 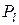относятся к линейной части функционала и соответствуют узловым неизвестным 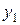и 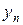, изгибающие моменты 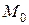и 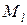также относятся к линейной части функционала и соответствуют узловым неизвестным 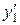и 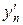, следовательно, для их учета требуется коррекция глобального вектора нагрузки в виде:

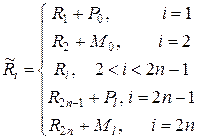, (32)

Таким образом, решение исходной задачи методом конечных элементов сводится к решению системы линейных алгебраических уравнений относительно узловых неизвестных:

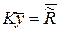(33)

3. Пример расчета.

В качестве модельного примера рассмотрим балку на упругом основании со следующими параметрами: 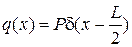, 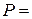100 кН – нагрузка, заданная в средней точке (см. рис. 5.); 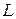=8 м, h_b=1.3 м, b_b=1 м;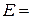 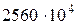кН/м² ; 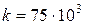кН/м³ .

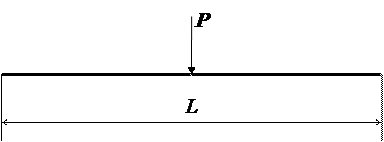
Рис. 5. К постановке рассматриваемой краевой задачи.

При этом будем рассматривать следующие краевые условия:

1. 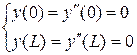– балка, шарнирно опертая с двух сторон,

2. 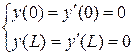– балка жестко закреплена с двух сторон,

3. 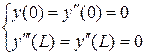– балка, шарнирно опертая слева, правый конец свободный,

4. 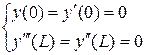– балка жестко закреплена слева, правый конец свободный.

Отметим, что в этом случае

, .

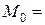
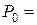
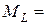
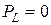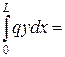
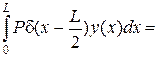
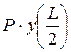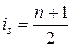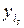
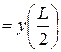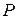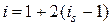
Поскольку нагрузка задана в средней точке, т.е. в среднем узле, следовательно, количество узлов должно быть нечетным. Тогда номер среднего узла . Порядковый номер узлового неизвестного , которому соответствует узловая нагрузка , 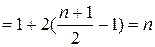. Следовательно, глобальный вектор нагрузки может быть сформирован без локальных построений, т.е.

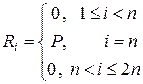(34)

⇐ Предыдущая 1 2 345 6 7 Следующая ⇒