
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Локальные построения на i-ом элементе.
2.1. Локальные построения на i-ом элементе.
Переходим к локальным координатам: 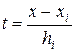 ,
, 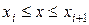 . При этом имеют место следующие соотношения:
. При этом имеют место следующие соотношения:
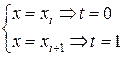 ,
, 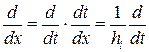 ,
, 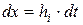 .
.
Представим неизвестную функцию прогиба 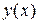 в виде кубической параболы
в виде кубической параболы
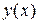
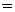
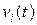
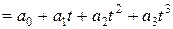 ,
, 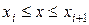 (6)
(6)
Для определения 4-х параметров 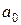 ,
, 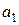 ,
, 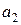 ,
, 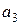 воспользуемся 4-мя узловыми значениями:
воспользуемся 4-мя узловыми значениями:
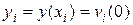 ,
, 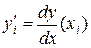
 ,
,
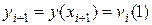 ,
, 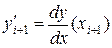
 .
.
Поскольку 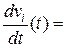
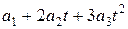 , получаем следующую систему линейных алгебраических уравнений относительно параметров
, получаем следующую систему линейных алгебраических уравнений относительно параметров 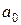 ,
, 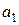 ,
, 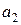 ,
, 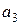 :
:
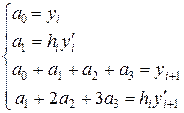 (7)
(7)
Введем следующие обозначения
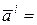
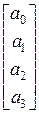 ,
, 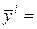
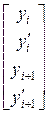 ,
, 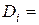
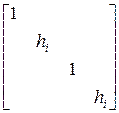 ,
, 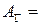
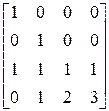 .
.
Тогда система уравнений (7) может быть представлена в матрично-векторном виде:
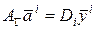 (8)
(8)
Следовательно
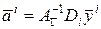
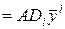 , где
, где 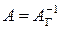 (9)
(9)
Легко проверить, что
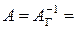
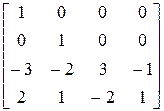 (10)
(10)
Обозначим 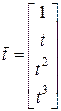 , тогда
, тогда 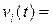
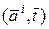
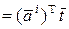
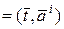
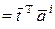 – скалярное произведение векторов
– скалярное произведение векторов 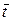 и
и 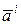 . Рассмотрим вычисление производных.
. Рассмотрим вычисление производных.
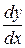


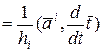 ,
,
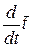
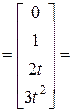

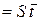 , где
, где 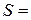
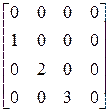
Т.е.
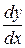
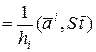
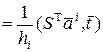 (11)
(11)
Далее
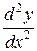
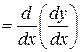
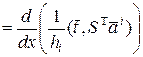
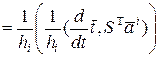
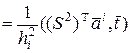 , (12)
, (12)
где 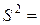
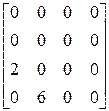
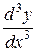
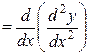
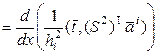
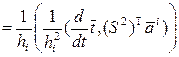
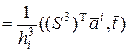 ,(13)
,(13)
где 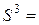

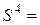
 и
и 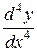

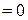 (14)
(14)
2.2. Построение локальной матрицы жесткости на i-ом элементе.
С учетом представленных выше локальных построений вычислим квадратичную часть функционала 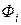 :
:
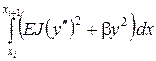 (15)
(15)
Рассмотрим общий случай 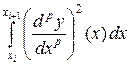 ,
, 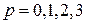
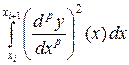
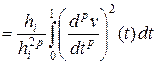
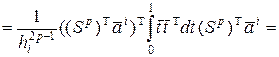
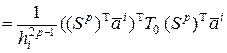
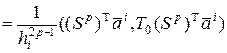 ,
,
где
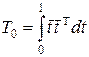
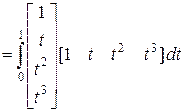
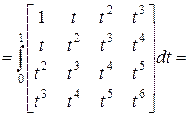
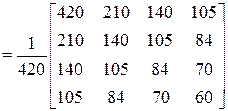 .
.
Следует заметить, что 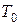
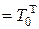 – симметричная матрица. Тогда
– симметричная матрица. Тогда
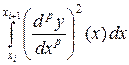
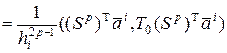
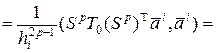
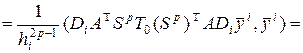
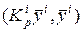 , где
, где
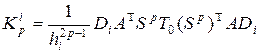 (16)
(16)
При 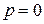
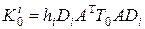 (17)
(17)
При 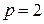
 (18)
(18)
Таким образом 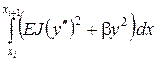
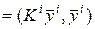 , где
, где
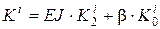 – локальная матрица жесткости (19)
– локальная матрица жесткости (19)
2.3. Построение локального вектора нагрузки на i-ом элементе.
С учетом представленных выше локальных построений вычислим линейную часть функционала 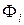 :
:
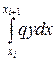 (20)
(20)
Рассмотрим в общем случае 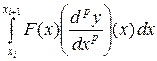 ,
, 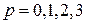 .
.
Полагаем, что 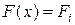 , например,
, например, 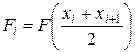 . Тогда
. Тогда
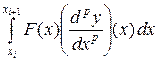
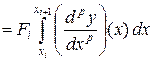
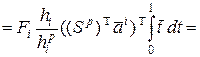
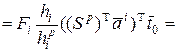
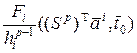

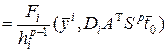
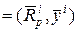 , где
, где 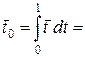
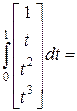
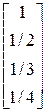

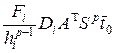 ,
, 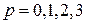 (21)
(21)
При 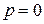
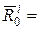
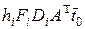 (22)
(22)
Таким образом,

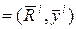 , где
, где 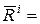
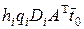 – локальный вектор нагрузки (23)
– локальный вектор нагрузки (23)
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|