
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
ЧИСЛЕННОЕ Решение задачи об изгибе балки на упругом основании методом конечных элементов
ЧИСЛЕННОЕ Решение задачи об изгибе балки на упругом основании методом конечных элементов
Предварительное замечание.
Пусть задан функционал вида
 , (1)
, (1)
где 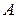 – симметричная
– симметричная 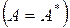 положительно определенная матрица, т.е.
положительно определенная матрица, т.е. 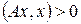 при всех
при всех 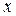 . Свойство положительной определенности соответствует положительности всех собственных чисел матрицы
. Свойство положительной определенности соответствует положительности всех собственных чисел матрицы 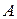 . Найти
. Найти 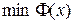 .
.
Условие минимума 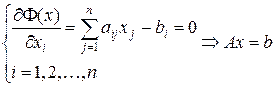 , (2)
, (2)
т.е. существует взаимно однозначное соответствие между задачей о минимуме функционала (1) и системой линейных уравнений Ax = b.
1. Общая постановка задачи об изгибе балки на упругом основании (модель Винклера).
Суть модели Винклера состоит в предположении, что реакция основания 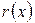 в произвольной точке балки x пропорциональна ее прогибу в этой точке:
в произвольной точке балки x пропорциональна ее прогибу в этой точке: 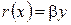 . Поэтому графически такую модель можно представить пружинками, не связанными друг с другом, каждая из которых имеет жесткость, пропорциональную прогибу балки в этой точке (рис. 1).
. Поэтому графически такую модель можно представить пружинками, не связанными друг с другом, каждая из которых имеет жесткость, пропорциональную прогибу балки в этой точке (рис. 1).
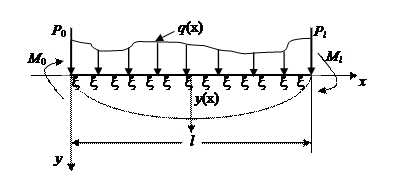
Рис. 1. Расчетная схема балки.
Напряженно-деформируемое состояние такой балки соответствует решению задачи о минимуме следующего функционала (функционала энергии): функция прогибов балки y(x), вызванных силами P, распределенной нагрузкой q и изгибающими моментами M, является условием минимума функционала энергии балки (т.е. принесет минимальное значение этому функционалу)
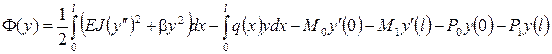 (3)
(3)
где
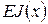 – жесткость балки при изгибе (изгибная жесткость);
– жесткость балки при изгибе (изгибная жесткость);
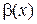 – коэффициент упругости основания (коэффициент постели);
– коэффициент упругости основания (коэффициент постели);
 ,
, 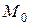 ,
,  ,
, 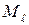 ,
, 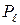 – заданные нагрузки.
– заданные нагрузки.
Замечание. Из курса вариационного исчисления следует, что решение такой задачи совпадает с решением следующей краевой задачи:
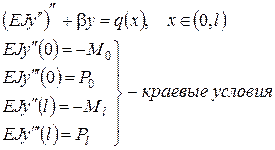 , (4)
, (4)
что соответствует исходной постановке, обычно формулируемой в курсе «Сопротивление материалов».
2. Метод конечных элементов (МКЭ).
Разобьем отрезок 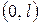 , занимаемый балкой, на (
, занимаемый балкой, на ( 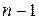 ) частей (элементов);
) частей (элементов);  – координаты точек разбиения,
– координаты точек разбиения, 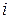 – номер точки,
– номер точки, 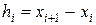 – длина
– длина 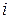 -го элемента (рис. 2).
-го элемента (рис. 2).
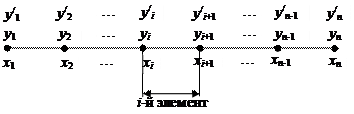
Рис. 2. Конечно-элементная разбивка.
В каждой 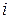 -ой точке разбиения примем в качестве неизвестных
-ой точке разбиения примем в качестве неизвестных 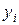 и
и 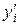 ,
,  , т.е. всего
, т.е. всего 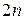 -неизвестных.
-неизвестных.
При этом
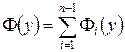 , (5)
, (5)
где 
здесь 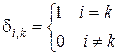 – символ Кронекера.
– символ Кронекера.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|