Построение глобальной матрицы жесткости и вектора нагрузки разрешающей системы.

2.4. Построение глобальной матрицы жесткости и вектора нагрузки разрешающей системы.

Общий функционал, представляющий сумму функционалов по элементам, с учетом представленных выше локальных построений примет вид

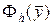
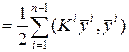
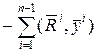, (24)

где 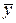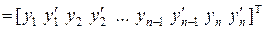– вектор узловых неизвестных.

Объединяя коэффициенты локальных матриц жесткости и компоненты локальных векторов нагрузок, относящихся к общим узловым значениям, получим

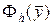
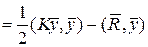(25)

где матрица 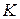называется глобальной матрицей жесткости, а вектор – глобальным вектором нагрузки.

Схематично формирование элементов матрицы 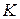представлено на рисунке 3.

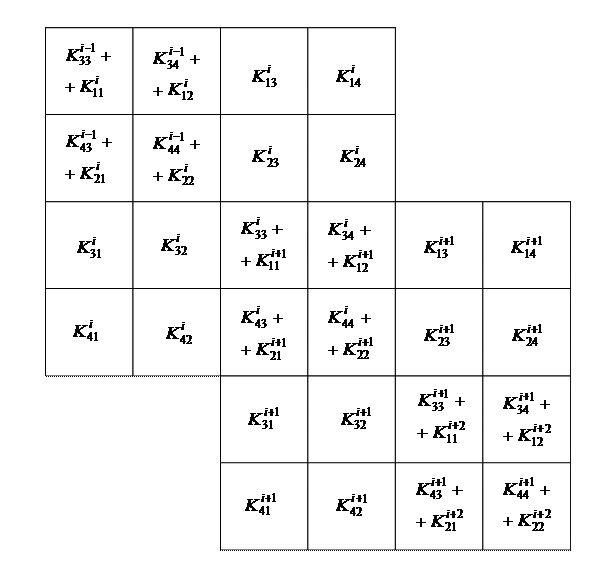
Рис. 3. К формированию глобальной матрицы жесткости.

Замечания к рисунку 3.

1. 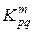– элементы локальной матрицы жесткости на 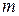-ом элементе:

, .

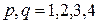2. При

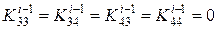
3. При ,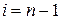

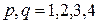
4. При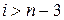

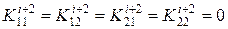
5. Представленный фрагмент матрицы 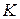отображает коэффициенты при узловых неизвестных 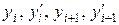и частично .

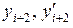Схематично формирование элементов вектора 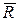представлено на рисунке 4.

Рис. 4. К формированию глобального вектора нагрузки.

Замечания к рисунку 4.

1. – элементы локального вектора нагрузки на 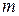-ом элементе: , .

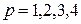2. При .

3. При .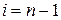

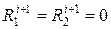4. Представленный фрагмент вектора 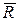соответствует в линейной части функционала узловым неизвестным .

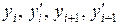2.5. Учет закреплений.

Пусть для некоторого узла с номером 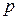, 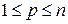задано условие

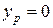(26)

Этому номеру соответствует порядковый номер неизвестной :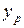

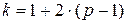(27)

Тогда для выполнения условия (26) следует приравнять нулю строку и столбец глобальной матрицы, имеющих номер 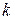, на главной диагонали вставить единицу, кроме того, обнулить 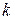-ю компоненту глобального вектора нагрузки:

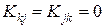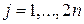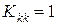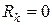, , , . (28)

Если задано условие

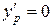, (29)

Тогда порядковый номер неизвестной 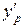имеет вид:

(30)

Для выполнения условия (29) требуется произвести аналогичную предыдущему случаю коррекцию глобальной матрицы и глобального вектора нагрузки (см. формулы (28), где порядковый номер 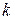неизвестной 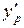представлен формулой (30)).

⇐ Предыдущая 1 234 5 6 7 Следующая ⇒