Хелпикс

Главная

Контакты

Случайная статья



Ответ: точка пересечения ( ; ; ).

⇐ ПредыдущаяСтр 4 из 4


Ответ: .

Задание №16

Найти точку пересечения прямой 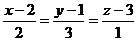 с плоскостью .

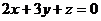Решение.

Параметрические уравнения прямой имеют вид

,

,

.

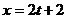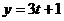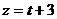Для определения точки пересечения прямой и плоскости подставим выражения для x, y, z из уравнения в уравнение плоскости. Получаем

,

,

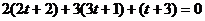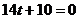откуда находим

.

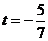Следовательно, координаты точки пересечения будут:

,

,

.

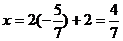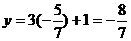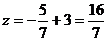Итак, прямая и плоскость пересекаются в точке ( ; ; ).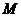

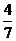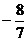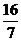Ответ: точка пересечения ( ; ; ).

Задание №17

Дана система линейных уравнений:

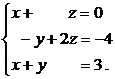
Решить эту систему:

а) по формулам Крамера,

б) с помощью обратной матрицы.

Решение.

а) Найдем определитель, состоящий из коэффициентов перед переменными:

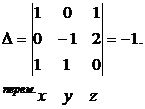
Посчитаем определитель, у которого 1-ый столбец заменяется столбцом свободных членов:

.

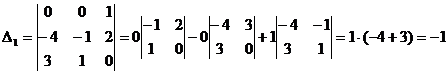Посчитаем определитель, у которого 2-ой столбец заменяется столбцом свободных членов:

.

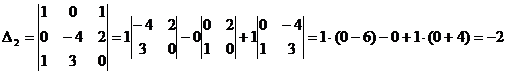Посчитаем определитель, у которого 3-ой столбец заменяется столбцом свободных членов:

.

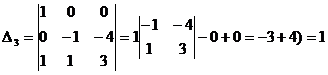Найдем значения x, y и z по формулам Крамера:

;

;

.

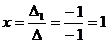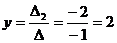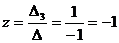Ответ: , , .

б) Рассмотрим матрицы:

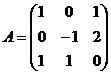- матрица, состоящая из коэффициентов перед переменными;

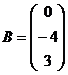  - матрица, состоящая из свободных членов;

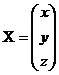    - матрица, состоящая из неизвестных.

Тогда, в матричной форме система линейных уравнений может быть записана следующим образом:

.

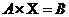Если 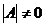, то система имеет единственное решение, которое можно найти по формуле:

,

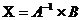где 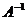 - обратная матрица к матрице 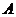. Найдем .

.

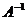Найдем определитель матрицы A:

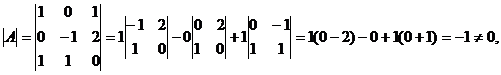
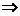 обратная матрица существует.

Определим алгебраические дополнения :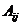

; ;  ;

; ;  ;

;  ; .

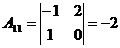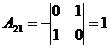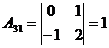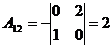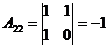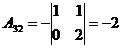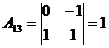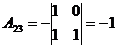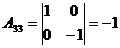Посчитаем :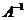

.

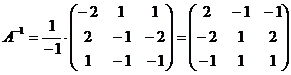Найдем :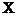

.

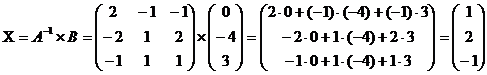Ответ: , , .


⇐ Предыдущая1234
  

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.