
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ СТРОИТЕЛЬНЫЙ УНИВЕРСИТЕТ
МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ СТРОИТЕЛЬНЫЙ УНИВЕРСИТЕТ
_
Кафедра высшей математики
векторная алгебра и аналитическая геометрия
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
К ПРАКТИЧЕСКИМ ЗАНЯТИЯМ И
ВЫПОЛНЕНИЮ РАСЧЕТНОГО ЗАДАНИЯ
ДЛЯ СТУДЕНТОВ ЗАОЧНОГО ОТДЕЛЕНИЯ
Москва 2007
С о с т а в и т е л и:
доцент, кандидат физико-математических наукТ.А.Мацеевич
Примеры решения задач по векторной алгебре и аналитической геометрии
Задание №1
Разложить вектор 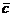 = {9, 4} по векторам
= {9, 4} по векторам 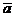 = {2, -3} и
= {2, -3} и 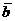 = {1, 2}.
= {1, 2}.
Решение.
Найдем коэффициенты 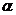 и
и 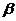 в разложении:
в разложении: 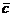 =
= 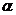
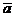 +
+ 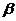
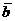 .
.
Запишем эту формулу в координатах. Сначала вычислим координаты правой части:
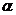
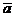 +
+ 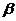
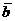 = {2
= {2 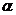 ; -3
; -3 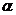 } + {1
} + {1 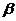 ; 2
; 2 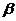 } = {2
} = {2 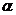 +
+ 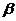 ; -3
; -3 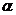 + 2
+ 2 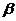 }.
}.
Эти координаты должны равняться соответствующим координатам вектора 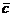 , следовательно:
, следовательно: 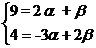 .
.
Решим эту систему уравнений методом исключения переменных.
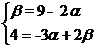
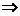
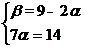
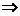
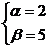
Ответ: = 2 + 5 .
Задание №2
Проверить коллинеарность векторов 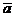 = {2, -1, 3} и
= {2, -1, 3} и 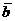 = {-6, 3, -9}.
= {-6, 3, -9}.
Решение.
Если векторы 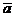 и
и 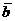 коллинеарны, то их координаты должны быть пропорциональны. Проверим это.
коллинеарны, то их координаты должны быть пропорциональны. Проверим это.
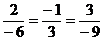 , т.е коэффициент пропорциональности существует и равен
, т.е коэффициент пропорциональности существует и равен 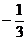 .
.
Ответ: II .
Задание №3
Дан вектор 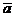 = {2, -1, 3}. Найти модуль вектора
= {2, -1, 3}. Найти модуль вектора 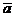 , координаты его орта
, координаты его орта 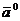 и направляющие косинусы.
и направляющие косинусы.
Решение.
а) Найдем модуль вектора 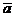 :
:
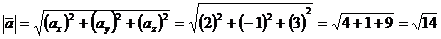 .
.
б) Найдем координаты орта 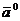 :
:
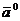 =
= 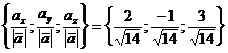 .
.
в) Найдем направляющие косинусы вектора 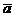 :
:
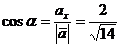 ;
;
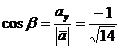 ;
;
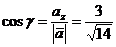 .
.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|