
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Ответ: т.к. , данные прямые параллельны.
Ответ: .
Задание №11
Две прямые заданы уравнениями 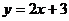 и
и 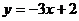 . Найти угол между этими прямыми.
. Найти угол между этими прямыми.
Решение.
Угловые коэффициенты данных прямых:
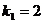
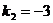 .
.
Поэтому по формуле
 ,
,
находим
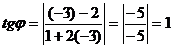 .
.
Таким образом, угол между данными прямыми равен
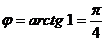 .
.
Ответ: .
Задание №12
Показать, что прямые 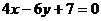 и
и 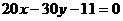 параллельны.
параллельны.
Решение.
При приведении уравнения каждой прямой к виду
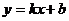
получаем:
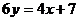 или
или 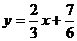 ;
;
и
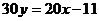 или
или 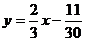 .
.
Откуда видно, что угловые коэффициенты 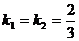 .
.
Следовательно, прямые параллельны.
Ответ: т.к. , данные прямые параллельны.
Задание №13
Показать, что прямые 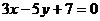 и
и 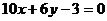 перпендикулярны.
перпендикулярны.
Решение.
Приведя уравнения каждой прямой к виду
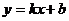
получаем:
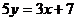 или
или 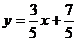 , где
, где 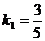 - угловой коэффициент,
- угловой коэффициент,
и
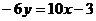 или
или 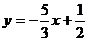 , где
, где 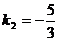 - угловой коэффициент.
- угловой коэффициент.
Откуда видно, что угловые коэффициенты 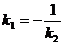 .
.
Следовательно, прямые перпендикулярны.
Ответ: т.к. , данные прямые перпендикулярны.
Задание №14
Составить уравнение плоскости проходящей через точку 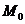 (1; 1; 1) перпендикулярно вектору
(1; 1; 1) перпендикулярно вектору 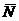 {2; 2; 3}.
{2; 2; 3}.
Решение.
По формуле
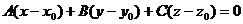 ,
,
где 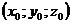 - координаты точки, лежащей в плоскости, а
- координаты точки, лежащей в плоскости, а 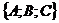 - координаты вектора, перпендикулярного данной плоскости, искомое уравнение будет:
- координаты вектора, перпендикулярного данной плоскости, искомое уравнение будет:
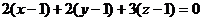 ,
,
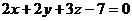 .
.
Ответ: .
Задание №15
Найти каноническое уравнение прямой заданной пересечением плоскостей:
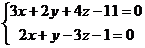 .
.
Решение.
Полагая, например, 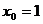 , из системы
, из системы
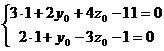 или
или 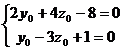
получаем
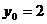 и
и 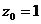
Таким образом, точка 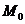 (1; 2; 1) искомой прямой найдена.
(1; 2; 1) искомой прямой найдена.
Теперь определим направляющий вектор 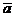 . Так как прямая определена пересечением плоскостей, то она перпендикулярна каждому из нормальных векторов
. Так как прямая определена пересечением плоскостей, то она перпендикулярна каждому из нормальных векторов 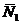 и
и 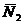 . Поэтому, в качестве вектора
. Поэтому, в качестве вектора 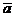 можно взять любой вектор, перпендикулярный векторам
можно взять любой вектор, перпендикулярный векторам 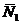 и
и 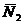 , например их векторное произведение
, например их векторное произведение 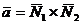 .
.
Так как координаты векторов известны:
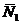 = {3; 2; 4}
= {3; 2; 4}
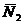 = {2; 1; -3},
= {2; 1; -3},
то
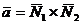
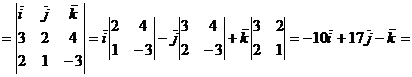 {-10; 17; -1}
{-10; 17; -1}
или
 = -10,
= -10, 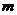 = 17,
= 17, 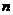 = -1.
= -1.
Подставляя найденные значения 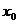 ,
, 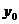 ,
, 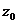 и
и  ,
, 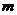 ,
, 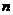 в равенства:
в равенства:
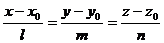 ,
,
получаем каноническое уравнение данной прямой:
 .
.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|