
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Задача №2.. Задача №3.. Задача №4.. Задача №5.
Задача №2.
Имеется сплав серебра с медью. Вычислите массу сплава и процентное содержание серебра в нем, зная, что сплавив его с 3кг чистого серебра, получается сплав, содержащий 90% серебра, а сплавив его с 2кг чистого серебра, получается сплав, содержащий 86% серебра.
Решение:
X кг – масса исходного сплава
(X+3)кг – масса первого сплава
(X+2)кг – масса второго сплава
(X+3)*0.9(кг) – содержание серебра в первом сплаве
(X+2)*0.86(кг) – масса серебра во втором сплаве
(X+3)*0.9-(X+2)*0.86=1
X=0.5
Табличный способ:
По первому предложению составляем таблицу
| Объект | I | II | Смесь |
| m кг | x | 3+x | |
| % серебра | p | ||
| mсеребра кг | x*p/100 | 3*100/100 | (3+x)*90/100=x*p/100+3*100/100 |
По второму предложению составляем таблицу
| Объект | I | II | Смесь |
| m кг | x | 2+x | |
| % серебра | p | ||
| mсеребра кг | x*p/100 | 2*100/100 | (2+x)*86/100=x*p/100+2*100/100 |
В результате в «желтых» клетках имеем уравнения для системы:
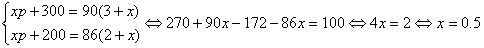
Тогда 0,5p=15, p=30
Ответ: 0,5 кг; 30 % серебра.
Задача №3.
Из 50т руды получают 20т металла, который содержит 12% примесей. Сколько процентов примесей содержит руда?
Решение:
Табличный способ:
| Объект | I | II | Получили |
| m тн | 50-20=30 | ||
| % примесей | p | ||
| mпримесей тн | 50*p/100 | 20*12/100=50*p/100-30 |
12*20=50p-3000
50p=3240
p=64.8
Ответ: 64.8%.
Задача №4.
Сплав меди и цинка весом 60 кг содержит 40% меди. Сколько нужно добавить цинка, чтобы в сплаве его концентрация достигла 80%.
Решение:
Табличный способ:
| Объект | I | II | Получили |
| m кг | x | 60+x | |
| % цинка | 100-40=60 | ||
| mцинка кг | 60*60/100 | x | (60+x)*80/100=60*60/100+x |
Имеем:
(60+x)*0.8=36+x
48+0.8x=36+x
x=60 кг цинка нужно добавить.
Задача №5.
К 15 литрам 10%-ого раствора соли добавили 5%-ный раствор соли и получили 8%-ный раствор. Какое количество литров 5%-ного раствора добавили?
Решение:
1) Пусть добавили Xл 5%-ного раствора соли.
(15+X)л – столько стало нового раствора
(15+X)*0.08л – столько в нем содержится соли
2) В 15 литрах 10%-ного раствора содержится
15*0.1=1.5(л) соли
3) В Xл 5%-ного раствора содержится 0.05Xл соли
X=10.
Добавили 10л 5%-ного раствора соли.
Табличный способ:
| Объект | I | II | Получили |
| m л | x | 15+x | |
| % соли | |||
| mсоли л | 15*10/100 | x*5/100 | (15+x)*8/100=15*10/100+5x/100 |
Имеем:
8(15+x)=150+5x
3x=30
x=10
Ответ: 10л
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|