Решение. Решение. Задача №1.

Решение

Итак, у нас есть три вещества:

1. 4 литра 15-процентного раствора;

2. 6 литров 25-процентного раствора;

3. Третий раствор с неизвестной концентрацией.

Составим таблицу:

	Общая масса, кг	Масса чистого вещества, кг
Раствор 1 (15%)		0,15 · 4 = 0,6
Раствор 2 (25%)		0,25 · 6 = 1,5
Раствор 3	x	y

По условию, нам не дана ни масса нового раствора, ни масса чистого вещества в нем. Поэтому обозначим общую массу x, а массу основного вещества y.

Поскольку при смешивании все массы складываются, получаем уравнения:

4 + 6 = x ⇒ x = 10;
0,6 + 1,5 = y ⇒ y = 2,1.

Уравнения получились настолько простыми, что даже не пришлось составлять систему. Но это еще не ответ! В задаче требуется найти концентрацию нового раствора. Чтобы найти ее, разделим массу чистого вещества на общую массу раствора:

y : x = 2,1 : 10 = 0,21

Итак, доля чистого вещества равна 0,21. Чтобы перевести долю в проценты, умножим на сто:

0,21 · 100 = 21

Ответ: 21.

Задача. Смешав 30-процентный и 60-процентный растворы кислоты и добавив 10 кг чистой воды, получили 36-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 41-процентный раствор кислоты. Сколько килограммов 30-процентного раствора использовали для получения смеси?

Решение

Обозначим массу 30-процентного раствора x, а массу 60-процентного раствора y. Получим таблицу:

	Общая масса, кг	Масса чистого вещества, кг
Раствор 1 (30%)	x	0,3x
Раствор 2 (60%)	y	0,6y
Чистая вода
Раствор 3 (50%)		0,5 · 10 = 5
Смесь «30% + 60% + вода»	x + y + 10	0,3x + 0,6y + 0
Смесь «30% + 60% + 50%»	x + y + 10	0,3x + 0,6y + 5

По условию, концентрация смеси «30% + 60% + вода» равна 36%. Получаем уравнение:

0,3x + 0,6y + 0 = 0,36 · (x + y + 10)

Аналогично, концентрация смеси «30% + 60% + 50%» равна 41%. Отсюда получаем еще одно уравнение:

0,3x + 0,6y + 5 = 0,41 · (x + y + 10)

Решаем полученную систему, вычитая первое уравнение из второго:

Теперь вспомним, что надо найти. А нужна масса 30-процентного раствора. Та самая, которую мы обозначили за x. Следовательно, x = 60 — это и есть ответ.

Ответ: 60.

Задача №1.

Сплав меди и цинка весом 20 кг содержит 30% меди. Добавили 22кг цинка. Сколько нужно добавить меди, чтобы в сплаве стало 60% цинка.

Очень удобно в задачах на сплавы, смеси, концентрации составлять таблицу по условию задачи (жирным шрифтом), а затем заполнять пустые клетки, руководствуясь законом сохранения массы(объема) и формулами расчета «Процент от числа». Для начала нужно определить количество объектов, которые участвуют в условии задачи ( в нашем случае их 4), затем занести в таблицу все, что говорится о каждом объекте. По вопросу задачу вводится переменная ( в нашем случае это x кг меди)

Объекты	I	добавили цинка	добавили меди	получили сплав
масса (кг)			x	20+22+x
% меди
% цинка
масса меди (кг)
масса цинка (кг)

Теперь начинаем заполнение пустых клеток:

Объекты	I	добавили цинка	добавили меди	получили сплав
масса (кг)			x	20+22+x=42+x
% меди				100-60=40
% цинка	100-30=70
масса меди (кг)	(20*30)/100		x	(42+x)40/100=(2030)/100+0+x
масса цинка (кг)	(20*70)/100

Нам, в принципе, достаточно заполнения четырех строк, чтобы составить уравнение.

Обратим внимание на «желтую» клетку- эта клетка является ключом составления уравнения задачи, т.к. мы ее можем заполнить по формуле «40 % от числа 42+x», а также по закону сохранения массы: (20*30)/100+0+x.

Следовательно, имеем уравнение: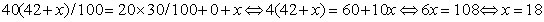

Ответ: 18.

⇐ Предыдущая 123 4 5 6 Следующая ⇒