Хелпикс

Главная

Контакты

Случайная статья



Задача 20.

⇐ ПредыдущаяСтр 4 из 5Следующая ⇒


Задача 20.

Решить однородную систему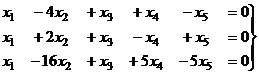

Решение.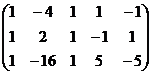

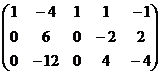
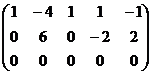 Ранг основной матрицы равен 2. Можно Оставить слева 2 переменных, например, 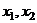, остальные свободные.

  

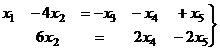
Из второго: 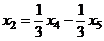 , подставим в 1-е.

.

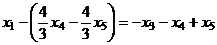Тогда  = .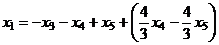 

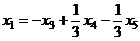Общее решение:  ,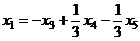

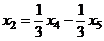
или в векторном виде: .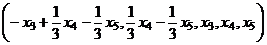

ФСР: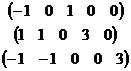

Ответ.

Общее решение: .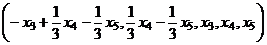

ФСР: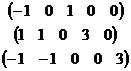

Задача 21. Решить однородную систему, найти ФСР.

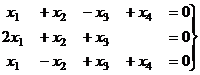
Решение.Преобразуем методом Гаусса основную матрицу системы.

 

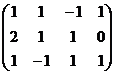
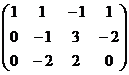
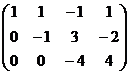
Треугольная структура продолжилась до самой последней строки, и не проявилась строка из нулей, то есть ранг равен 3. Здесь всего одна свободная переменная. Развернём обратно эту матрицу, т.е. запишем в виде системы, а затем перенесём свободные переменные вправо. 

 

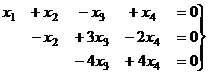
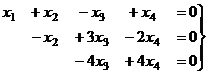
Из последнего, 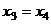, это подставим во 2-е и получим .

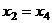Затем это всё в 1-е уравнение, получим .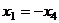

ФСР: один вектор .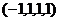

Ответ.Общее решение: 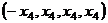. ФСР: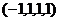

Задача 22. Решить однородную систему, найти ФСР.

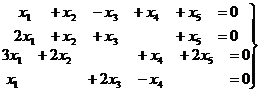
Решение.Преобразуем методом Гаусса основную матрицу системы.

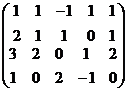
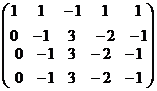     далее можно вычесть 2 строку из 3-й и 4-й, и там везде будут 0.

Здесь ранг 2, неизвестных 5, .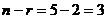

Переписывая в виде системы, переносим вправо 3 свободных переменных.

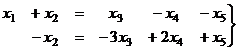
Выражаем из 2-го 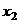 как линейную функцию от 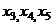, а затем с помощью 1-го уравнения, также и .

, . 

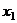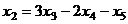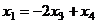Общее решение: .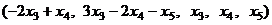

ФСР из 3 векторов. Для этого задаём поочерёдно 1 какой-либо из свободных переменных, а 0 остальным.

ФСР: , , .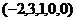

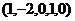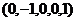Ответ.Общее решение: .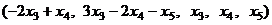

ФСР: , , .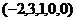

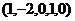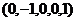Задача 23. Решить однородную систему, найти ФСР: 

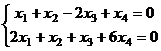
Решение. Сначала быстро преобразуем основную матрицу методом Гаусса, для чего из 2 строки вычтем удвоенную 1-ю.

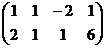
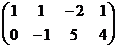 , видим, что базисный минор в 1 и 2 столбцах, тогда  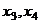свободные переменные.

Система после преобразования: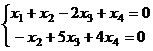

Переносим вправо :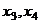   

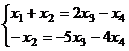
Последнее уравнение будет логично умножить на коэффициент .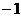

Тогда 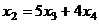, подставляя эту информацию в 1-е уравнение, получим , тогда .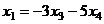

Запишем общее решение , ,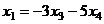

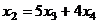оно же в векторном виде: .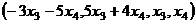

Поочерёдно присваивая 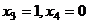, затем 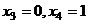, получим два вектора: (-3,5,1,0) и (-5,4,0,1).

Ответ.Общее решение , .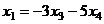

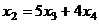ФСР (-3,5,1,0) и (-5,4,0,1).

Задача 24 или домашняя. 

Решить однородную систему, найти ФСР  

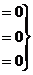
Ответ. Общее решение: 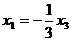, , 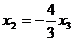ФСР: .

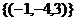Практика 12. (16 дек 932025, 19 дек 932024).

Повторение и контрольная работа по системам уравнений:

1) Определённая.

2) Неоднородная неопределённая

3) Однородная неопределённая.

(60-80 минут, почти вся пара).

 


⇐ Предыдущая12345Следующая ⇒
  

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.