
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Решение.. Задача 15.. Решение.. Однородные системы.. Практика 11 (15 дек 932025, 17 дек 932024)
Решение.
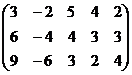




Вычёркивается лишнее 3-е уравнение.
Базисный минор не может быть в 1 и 2 столбце. Или 1 и 3, или 1 и 4. Лучше 1 и 4, чтобы делить на 5.

Получили систему:
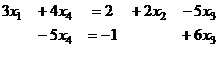
Из второго: 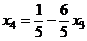 подставляем в 1-е:
подставляем в 1-е:
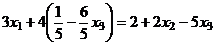
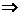
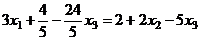
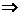
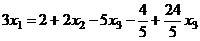
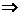
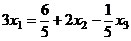
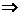
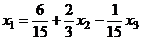 .
.
Общее решение: 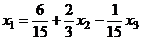 ,
, 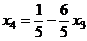
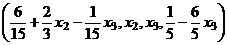 .
.
Частное решение: 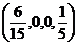 . Подставим во все 3 уравнения, проверим.
. Подставим во все 3 уравнения, проверим.
- - - Перерыв - - -
Задача 15.
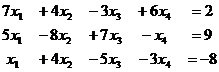
Решение.
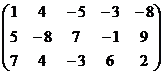

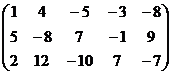

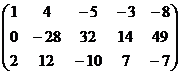

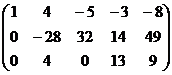

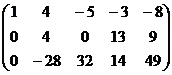

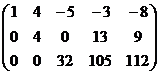
Получили систему:
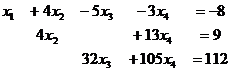
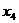 свободная переменная, базисный минор в 1,2,3 столбцах.
свободная переменная, базисный минор в 1,2,3 столбцах.

Из последнего: 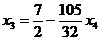 из второго:
из второго: 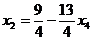 .
.
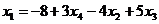 =
=  =
=
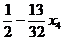 .
.
Общее решение:
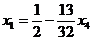 ,
, 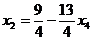 ,
, 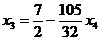 .
.
Однородные системы.
Задача 16. Решить однородную систему 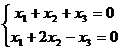 .
.
Решение.Можно записать основную матрицу и там вычесть 1-ю строку из 2-й, впрочем, можно для небольшой системы сделать это и сразу в системе, вычесть 1-е уравнение из 2-го. Получится:
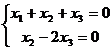
Ранг равен 2, а неизвестных 3, 3-я неизвестная свободная, переносим вправо. Тогда: 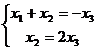
Из 2-го уравнения  , тогда
, тогда 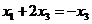 , а значит
, а значит 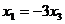 .
.
Общее решение: 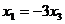 ,
,  . В виде вектора:
. В виде вектора: 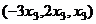 .
.
Присвоим 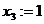 , получим остальные неизвестные.
, получим остальные неизвестные.
ФСР состоит всего из одного вектора: 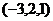 . Все остальные решения пропорциональны этому.
. Все остальные решения пропорциональны этому.
Если бы, например, присвоили  , получили бы
, получили бы 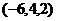 . Это потому, что всего одна свободная переменная.
. Это потому, что всего одна свободная переменная.
Ответ.Общее решение: 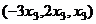 , ФСР
, ФСР 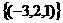 .
.
Практика 11 (15 дек 932025, 17 дек 932024)
Задача 17.Решить систему 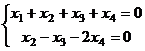
Решение.Минор, состоящий из 1 и 2 столбцов, уже в треугольной форме. Базисный минор порядка 2. Тогда 3-я и 4-я переменная - свободные. Перенесём их через знак равенства. 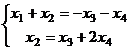 .
.
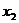 уже фактически выражено:
уже фактически выражено: 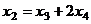 , подставим это в первое уравнение, чтобы выразить
, подставим это в первое уравнение, чтобы выразить 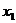 .
.
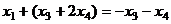
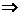
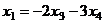 .
.
Общее решение: { 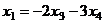 ,
, 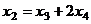 }.
}.
Если поочерёдно присвоить значение 1 каждой из свободных переменных (а другая в это время 0) то получим гарантированно 2 линейно-независимых вектора, они не пропорциональны, так как 1 на разных местах.
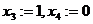 , получим
, получим 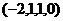
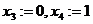 , получим
, получим 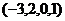 .
.
Эти 2 вектора { 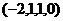 ,
, 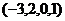 } и есть ФСР. Это
} и есть ФСР. Это  частных решений, из которых можно составить любые другие частные решения: любые их линейные комбинации будут частными решениями однородной системы.
частных решений, из которых можно составить любые другие частные решения: любые их линейные комбинации будут частными решениями однородной системы.
Ответ. Общее решение { 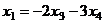 ,
, 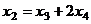 }.
}.
ФСР { 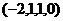 ,
, 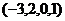 }.
}.
Замечание. Для системы с квадратной матрицей справа были только числа, для системы с прямоугольной матрицей к ним добавляются свободные переменные, и там будут выражения типа 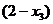 . А для однородной системы справа констант нет (они = 0), но туда перенесены свободные переменные. То есть идея решения методом Гаусса во всех этих 3 параграфах одна и та же, но справа разные типы объектов.
. А для однородной системы справа констант нет (они = 0), но туда перенесены свободные переменные. То есть идея решения методом Гаусса во всех этих 3 параграфах одна и та же, но справа разные типы объектов.
Задача 18. Решить однородную систему 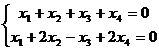
Решение. Запишем основную матрицу, преобразуем её. 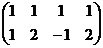

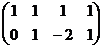
снова представим в виде системы: 
базисный минор порядка 2, можно обвести в левом углу, поэтому 3-я и 4-я переменная - свободные. Здесь их уже две, так как 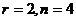 , поэтому
, поэтому 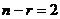 . Перенесём их через знак равенства.
. Перенесём их через знак равенства.
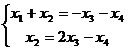
здесь 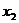 уже выражено:
уже выражено: 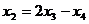 , подставим это в первое уравнение, чтобы выразить и
, подставим это в первое уравнение, чтобы выразить и 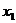 .
.
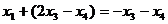 ,
, 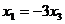 .
.
Общее решение: 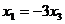 ,
, 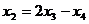 .
.
В виде вектора: 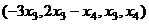 .
.
Если поочерёдно присвоить значение 1 каждой из свободных переменных (а другая в это время 0) то получим гарантированно 2 линейно-независимых вектора, они не пропорциональны, так как число 1 в них на разных местах.
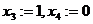 , получим
, получим 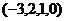
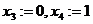 , получим
, получим 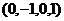 .
.
Эти 2 вектора { 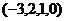 ,
, 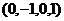 } и есть ФСР. Это
} и есть ФСР. Это  частных решений, из которых можно составить любые другие частные решения. Любые их линейные комбинации будут частными решениями однородной системы.
частных решений, из которых можно составить любые другие частные решения. Любые их линейные комбинации будут частными решениями однородной системы.
Ответ.Общее решение: 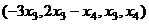 .
.
ФСР это множество из 2 векторов: { 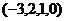 ,
, 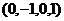 }.
}.
Задача 19. Решить однородную систему, найти ФСР. 
Решение. Запишем основную матрицу системы и преобразуем её методом Гаусса.
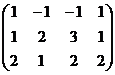

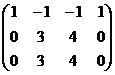

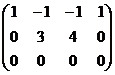
Ранг матрицы равен 2, базисные столбцы 1-й и 2-й. Несмотря на то, что сначала могло показаться, что здесь будет одна свободная переменная (4 переменных и 3 уравнения), на самом деле здесь будет две свободных переменных, ведь 3-е уравнение оказалось линейной комбинацией первых двух. 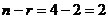 .
.
Снова возвращаемся от матрицы к системе уравнений. 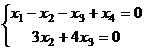
перенесём свободные неизвестные вправо:
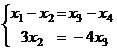 из 2 уравнения
из 2 уравнения 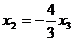 , подставим это в 1-е,
, подставим это в 1-е,
будет 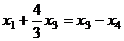 , то есть
, то есть 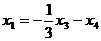 .
.
Общее решение: 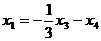 ,
, 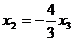 .
.
В виде вектора: 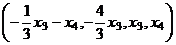
Построим ФСР из 2 векторов.
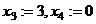 , получим
, получим 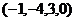
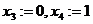 , получим
, получим 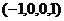 .
.
Так как здесь есть дроби, то для того, чтобы векторы в ФСР содержали только целые координаты, можно задавать не только 1, но и другое число, главное только чтобы в 3 и 4 координатах помещался невырожденный минор. Если мы задаём поочерёдно каждой свободной переменной какое-то число (не обязательно 1) а остальным 0, то линейная независимость этой системы векторов всё равно заведомо обеспечена.
Ответ. Общее решение: 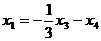 ,
, 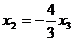 .
.
ФСР из 2 векторов:  .
.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|